Graph-based SLAM
基本概念
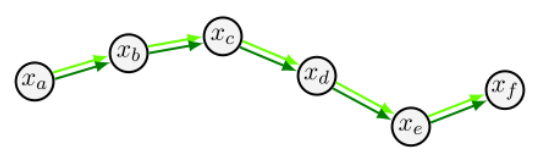
首先先简单介绍一下 Graph-SLAM 的基本数学概念。顾名思义, Graph-SLAM 就是基于一个图来进行 SLAM 的过程。这里提到的图是数学意义上的图,主要包含了两个概念:节点 (Node) 和边 (Edge)。节点用来表示我们想要关注的状态,而节点之间边则表示他们相对关系。在激光 SLAM 上,图里的节点表示的是不同时间下的机器人的状态,边这表示不同状态直接的相对位置关系。由于激光 SLAM 没有特征点检测,并且激光点本身的测距精度也比视觉 SLAM 来得高,所以只将机器人的位姿(在二维中是 $(x, y, \theta)$, 在三维中是 $(x, y, z, \theta_{roll}, \theta_{yaw}, \theta_{pitch})$)纳入到节点中,如下图所示。而在视觉 SLAM 中,还会把每一帧图像中检测出来的特征点也纳入到节点当中以便后续优化,如果还融合其他的传感器如 VIO,状态量还会将载体的速度和加速度也考虑在内。
节点和边的构建(前端)
有了关于位姿图的基本概念之后,我们来看一下图是怎么构建的。首先我们可以假定一个初始位置,然后在激光 SLAM 中,两个节点之间的边表示了两个状态之间的相对位置关系,这个在之前的笔记可知,有两种方法可以获得:既可以通过轮式里程计(如果有的话)来进行位姿变化的估算;也可以通过前后帧的帧间匹配来进行估算。这样都可以构建出一条边,并根据这条边(相对位置关系)构建出相连的节点;
上面提到的时候是构建两个相邻时间的节点之间的边;另外通过回环检测还能在两个不相邻的节点之间构建边。简单来说,回环检测是 通过一定方法(后面会详细介绍)发现图中的两个节点包含了一定位置关系(观测到了同一个对象等等) 这样通过观测到的同一对象,我们同样可以通过这两个时刻的点云进行帧间匹配获得一个相对位置关系,从而构建一条边。
图优化(后端)
假设在上图中,我们在 $x_b$ 和 $x_f$ 中检测出了回环,并构建出了一条边之后,我们可以发现,$x_b$ 和 $x_f$ 的相对位置关系我们有两种方法进行计算:
- 通过相邻点之间的位置关系计算出
$T_{b,c,...,f}$ - 通过回环检测构建出来的边:
$T_{bf}$
因为这两个状态是一个定值,理论上这两个相对位置关系应该相等,即 $T_{b,c,...,f}T^{-1}=I$。但是我们都知道,帧间匹配或者轮式里程计都存在一定误差,并且会随时间积累,所以前式几乎不可能成立,因此这个时候我们通过寻找一个最优配置(涉及到回环中的所有状态,在这个例子即 $b, c, d, e, f$)来使得这个误差(的平方)最小,这个过程就涉及到一个一个最小二乘问题,同时因为位姿计算之间有三角函数计算,所以是非线性的,所以优化的过程就是计算非线性最小二乘的计算。
非线性最小二乘原理
首先非线性最小二乘的原理和线性最小二乘比较类似,关于线性最小二乘的部分我之前在做关于轮式里程计标定的部分有记录过,详见:轮式里程计运动模型及标定。
问题引入
首先给定一个系统,其状态方程由 $f(x) = z$ 描述,其中:
$x$为该系统的状态向量,也是我们重点关注需要估计的值$z$为该系统的观测值,通常由传感器可以进行直接观测获得$f(x)$为该系统的关于状态向量$x$的一组映射非线性函数,也称为观测函数,表示$x$和$z$之间的对应关系
由于状态向量 $x$ 无法直接获得,因此我们的问题是,给定一组(带有噪声的)观测值 $(z_1, z_2, ..., z_n)$,如下所示:
$$
\begin{aligned}
f_1(\mathbf{x}) &= \mathbf{z}_1'\\
f_2(\mathbf{x}) &= \mathbf{z}_2'\\
...\\
f_n(\mathbf{x}) &= \mathbf{z}_n'
\end{aligned}\rightarrow
\begin{aligned}
\mathbf{z}_1\\
\mathbf{z}_2\\
...\\
\mathbf{z}_n
\end{aligned}
$$
我们需要估计(预测)一组状态向量 $x$,使得通过其观测方程计算出的预测观测值和实际观测值的误差最小,这个概念基本和线性最小二乘一致;区别只在于映射函数是线性还是非线性。
误差函数和目标函数
通过上述我们可以知道,我们的目标是最小化预测(观测值)和实际观测值的误差的平方。
首先误差可以定义如下(这是最简单的定义方法,对于一些非标量的观测量可能有不一样的计算方法,需要具体问题具体分析):
$$
e_i(\mathbf{x}) = f_i(\mathbf{x}) - z_i
$$
假设误差服从高斯分布,因此其对应的信息矩阵为 $\Omega_i = \Sigma^{-1}$,协方差矩阵定义为 $\Sigma_i$,因此我们可以把观测值误差的平方定义为:
$$
E_i(\mathbf{x}) = e_i(\mathbf{x})^T\Sigma^{-1}_ie_i(\mathbf{x})
$$
这里中间乘上协方差矩阵简单来说可以理解为其表示了不同边直接误差的权重,所以各边直接误差并不是简单相加,而是一直加权平方和。
因此,非线性最小二乘的目标函数为:
$$
F(\mathbf{x}) = \sum_i^N E_i(\mathbf{x}) = \sum_i^N e_i(\mathbf{x})^T\Sigma^{-1}_ie_i(\mathbf{x})
$$
而我们的目标是是求:$\arg\min_\mathbf{x}F(x)$
求解方法
方程线性化
首先最容易想到的方法就是通过方程求导令其为 0,然后求出 $\mathbf{x}$ 即可。我们在线性最小二乘方法中提到过这个方法,但是对于非线性函数,通常很难通过求导得到解析解,因此很自然可以想到:我们能否对其进行线性化,因此我们需要通过进行泰勒展开得到线性化方程。
考虑到 $F(\mathbf{x})$ 中只有 $e_i(\mathbf{x})$ 是一个非线性函数。我们可以直接对 $e_i(\mathbf{x})$ 进行线性化,对于某一个状态向量 $\mathbf{x}$,有:
$$
e_i(\mathbf{x} + \Delta\mathbf{x}) = e_i(\mathbf{x}) + J_i(\mathbf{x})\Delta\mathbf{x}
$$
其中根据泰勒展开式,$J$ 是该组映射函数对状态向量 $\mathbf{x}$ 的一阶导数,称为 Jacobian 矩阵。
$$
J_i(\mathbf{x}) = (\frac{\partial f_i(\mathbf{x})}{\partial x_1}, \frac{\partial f_i(\mathbf{x})}{\partial x_2}, ..., \frac{\partial f_i(\mathbf{x})}{\partial x_n})
$$
因此函数 $F(x)$ 线性化后为:
$$
F(\mathbf{x} + \Delta \mathbf{x}) = \sum e_i(\mathbf{x} + \Delta \mathbf{x})^T\Sigma^{-1}_i e_i(\mathbf{x} + \Delta \mathbf{x})
$$
化简求解
接下来可以对 $F(\mathbf{x} + \Delta \mathbf{x})$ 进行化简并求解:
$$
\begin{aligned}
F(\mathbf{x} + \Delta \mathbf{x}) &= \sum e_i(\mathbf{x} + \Delta \mathbf{x})^T\Sigma^{-1}_i e_i(\mathbf{x} + \Delta \mathbf{x}) \\
&= \sum (e_i(\mathbf{x}) + J_i \Delta \mathbf{x})^T \Sigma^{-1}_i (e_i(\mathbf{x}) + J_i\Delta \mathbf{x}) \\
&= \sum e_i^T\Sigma^{-1}_ie_i + e_i^T\Sigma^{-1}_iJ_i\Delta \mathbf{x} + \Delta \mathbf{x}^T J_i^T\Sigma^{-1}_i e_i + \Delta \mathbf{x}^TJ_i^T\Sigma^{-1}_iJ_i\Delta \mathbf{x} \\
&= \sum e_i^T\Sigma^{-1}_ie_i + 2e_i^T\Sigma^{-1}_iJ_i\Delta \mathbf{x} + \Delta \mathbf{x}^TJ_i^T\Sigma^{-1}_iJ_i\Delta \mathbf{x} \\
&= c_i + 2b_i^T\Delta \mathbf{x} + \Delta \mathbf{x}^T H_i \Delta \mathbf{x}
\end{aligned}
$$
可以发现,$F(\mathbf{x} + \Delta \mathbf{x})$ 是关于变量 $\Delta \mathbf{x}$ 的二次函数。对其求导有:
$$
\begin{aligned}
\frac{\partial F(\mathbf{x} + \Delta \mathbf{x})}{\partial \Delta \mathbf{x}} &= 2b + (H + H^T)\Delta \mathbf{x} = 0 \\
&= 2b + (J_i^T\Sigma^{-1}_iJ_i + J_i\Sigma^{-1}_i^TJ_i^T)\Delta \mathbf{x} = 0 \\
&= 2b + 2H\Delta \mathbf{x} = 0 \\
H\Delta \mathbf{x} &= -b \\
\Delta \mathbf{x}^* &= -H^{-1}b
\end{aligned}
$$
因此只要令 $\mathbf{x} = \mathbf{x} + \Delta \mathbf{x}$,然后通过迭代至收敛即可。
总结
总结一下以上流程,主要分成四步:
- 线性化误差函数:
$e_i(\mathbf{x} + \Delta \mathbf{x}) = e_i(\mathbf{x}) + J_i\Delta \mathbf{x}$ - 构建线性系统:
$b^T = \sum e_i^T\Sigma^{-1}_iJ_i$$H = \sum J_i^T\Sigma^{-1}_iJ_i$$H\Delta \mathbf{x} = b$
- 求解线性系统:
$\Delta \mathbf{x}^* = -H^{-1}b$ - 更新解直至收敛:
$\mathbf{x} = \mathbf{x} + \Delta \mathbf{x}^*$
非线性最小二乘在 SLAM 中的应用
图的构建
首先进行图的构建,根据第一部分的介绍,可以知道在激光 SLAM 中节点和边分别对应机器人在不同时间的位姿 $(x, y, \theta)$ 以及位姿之间的相对位置变化 $(dx, dy, d\theta)$。其中:
- 相邻节点之间的边通过里程计测量构建,这里的里程计可以是轮式里程计或者帧间匹配里程计(激光里程计),在视觉 SLAM 中也可以是视觉里程计;
- 不相邻节点之间的边要通过回环检测来构建,节点 i 和节点 j 观测到同样的环境信息,两者进行匹配得到相对位姿。并在对应的节点中连一条边,边为匹配的相对位姿。用信息矩阵来描述本次匹配的可靠性。
误差函数
- 预测观测值
$Z'_{ij}$:通过轮式里程计得到的相对位置关系可以作为相邻节点之间的预测值 - 实际观测值
$Z_{ij}$:通过两帧之间的帧间匹配得到的相对位姿可以作为实际观测值 - 因此误差函数
$e_{ij}(\mathbf{x}) = t2v(Z^{-1}Z')$,$t2v$在这里表示位姿矩阵转换为位姿向量
通过位姿计算可以得到误差函数的矩阵形式为,注意一下下标为 $ij$ 的值都是直接从观测值获取而来,而不是通过两个节点进行相对计算:
$$
e_{ij}(\mathbf{x}) =
\begin{bmatrix}
R_{ij}^T(R_i^T(t_j - t_i) - t_{ij}) \\
\theta_j - \theta_i - \theta_{ij}
\end{bmatrix}
$$
注意上面第一项是一个 $2\times 1$ 的向量,第三项的角度需要转到 $[-\pi, \pi]$ 上。
接下来求上述矩阵的 Jacobian 矩阵:
$$
\begin{aligned}
\frac{\partial e_{ij}(\mathbf{x})}{\partial x_i} &= \begin{bmatrix}
-R_{ij}^TR_i^T & R_{ij}^T\frac{\partial R_i^T}{\partial \theta}(t_j - t_i) \\
0 & -1
\end{bmatrix} \\
\frac{\partial e_{ij}(\mathbf{x})}{\partial x_j} &= \begin{bmatrix}
R_{ij}^TR_i^T & 0 \\
0 & 1
\end{bmatrix}
\end{aligned}
$$
线性化
我们的误差如下:
$$
\begin{aligned}
e_{ij}(\mathbf{x} + \Delta \mathbf{x}) &= e_{ij}(\mathbf{x}) + J_{ij}\Delta \mathbf{x} \\
J_{ij} = \frac{\partial e_{ij}(\mathbf{x})}{\partial \mathbf{x}}
\end{aligned}
$$
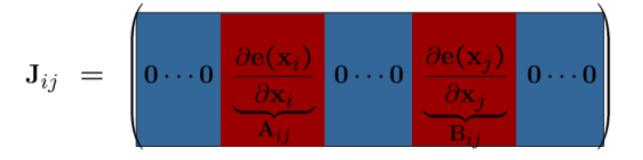
但是通过上一部分我们可以发现,对于误差函数 $e_{ij}$,他只对涉及到的两个节点 $\mathbf{x}_i$ 和 $\mathbf{x}_j$ 有关,因此有:
$$
\begin{aligned}
\frac{\partial e_{ij}(\mathbf{x})}{\partial \mathbf{x}} &= (0 ...\frac{\partial e_{ij}(\mathbf{x})}{\partial \mathbf{x}_i} ... \frac{\partial e_{ij}(\mathbf{x})}{\partial \mathbf{x}_j} ... 0) \\
J_{ij} &= (\mathbf{0} ... \mathbf{A}_{ij} ... \mathbf{B}_{ij} ... \mathbf{0})
\end{aligned}
$$
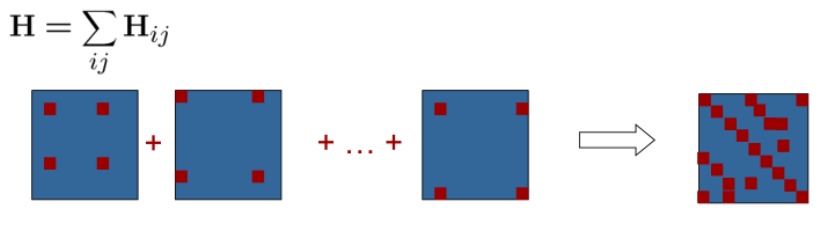
因此可以发现,Jacobian 矩阵是一个稀疏矩阵,因此由其组成的 H 矩阵也是一个稀疏矩阵,如下图所示:
因此得到 H 和 b 的最终形式为:
利用稀疏矩阵的特殊性,我们可以快速求解 $H\Delta \mathbf{x} = b$,这里不详细展开说。
坐标系固定
由于之前提到的边全都是相对位置关系,因此我们通过上面求出来的解是无穷多个;通常的做法是固定第一个位姿作为起始位姿,加入一个约束条件:$\Delta x_1 = 0$。展开如下:
加入一个约束:
$$
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix} \Delta x =
\begin{bmatrix}
0 \\
0 \\
0 \\
\end{bmatrix}
$$
求解的线性系统为:$H\Delta x = -b$
等价于:
$$
H_{11} +=
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix}
$$
构建线性系统
已知误差矩阵 $J$ 即 $(A_{ij}, B_{ij})$
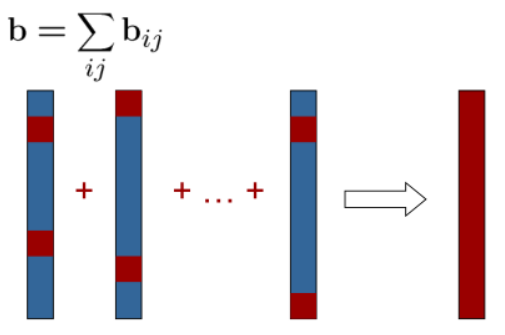
向量 $b$ 的更新为:
$$
\begin{aligned}
b_i^T &+= e_{ij}^T\Omega_{ij}A_{ij} \\
b_j^T &+= e_{ij}^T\Omega_{ij}B_{ij}
\end{aligned}
$$
矩阵 H 的更新为:
$$
\begin{aligned}
H_{ii} += A_{ij}^T\Omega_{ij}A_{ij} \\
H_{ij} += A_{ij}^T\Omega_{ij}B_{ij} \\
H_{ji} += B_{ij}^T\Omega_{ij}A_{ij} \\
H_{jj} += B_{ij}^T\Omega_{ij}B_{ij}
\end{aligned}
$$
求解
- 已知矩阵 H 和 向量 b
- 求解
$H\Delta x = -b$,这里要利用稀疏矩阵的特殊性进行矩阵,不要直接求逆 - 进行迭代,直至收敛