基于已知位姿的栅格构图算法

本文整理了三种基于栅格的建图方法，分别是覆盖栅格建图算法、计数建图算法和 TSDF 建图法。内容主要参考自深蓝学院的激光slam课程。

地图分类

在学习怎么建图之前需要先对地图的分类有个基本认识，这里主要介绍三中地图：

尺度地图（Matric Map）：在尺度地图中，每一个地点可以用一个坐标来表示，例如经纬度地图。栅格地图也是尺度地图的一种，在栅格地图中，环境被分割成一个个栅格；尺度地图中的距离和真实环境的距离是成一定比例的
拓扑地图（Topological Map）：拓扑地图由边和点组成，每个地点用一个点表示，地点之间的距离用边表示；相对于尺度地图，拓扑地图搜索速度更快，因为在尺度地图中我们必须通过不断搜索周围栅格来进行对目标搜索，哪怕当大部分栅格都是空的情况也需要这么操作，而在拓扑地图中，我们只需要搜索周围的点，来判断两个点之间是否有连通通路即可
语义地图（Semantic Map）：前两种地图对地点的表示方法都是点（栅格或者节点），而语义地图在这个点的基础添加标签

本文主要是以尺度地图作为建图的对象。

覆盖栅格建图算法

特点

将环境分解成一个个栅格
每个栅格有两种状态：占用（Occupied）、空闲(Free)，某些情况下我们还会添加未知（Unknown）也作为栅格状态的一种，表明不知道该栅格的占用情况
整个地图是一个非参模型，只用一系列孤立的栅格组成，没有通过某些参数来建模
天然区分可通行区域（栅格状态即可表示），适合进行轨迹规划
由于环境中每个点都需要用栅格表示，因此内存需求随地图增大急剧增加

待解决问题-数学描述

给定一系列机器人位姿和传感器观测数据，如下：

$$
\mathrm{data} = {x_1, z_1, x_2, z_2, ..., x_t, z_t}
$$

估计最有可能符合上述数据的地图：

$$
m* = \arg\max_m P(m|data) \\
\rightarrow m* = \arg\max_m P(m|x_{1:t}, z_{1:t})
$$

由于地图是有一系列栅格 $m_i$ 组成的，我们可以将栅格的状态也用二值随机变量表示：

$p(m_i) = 1$ 表示占用
$p(m_i) = 0$ 表示空闲

实际使用中可能会使用阈值而不是两个极端值来表示占用状态。同时我们假设建图过程中地图不会发生变换，并且每个栅格独立，因此有：

$$
p(m) = \prod p(m_i)
$$

因此地图估计问题最后可以表示为：

$$
P(m|x_{1:t}, z_{1:t}) = \prod p(m_i|x_{1:t}, z_{1:t})
$$

由此我们将整体地图估计问题转变为对每一个独立栅格的估计问题。

地图栅格估计过程

这一部分我们要估计： $p(m_{i}|x_{1:t},z_{1:t})$

首先由贝叶斯公式有：

$$
p(m_i|x_{1:t}, z_{1:t}) = \frac{p(z_t|m_i,z_{1:t-1},x_{1:t})p(m_i|z_{1:t-1},x_{1:t})}{p(z_t|z_{1:t-1},x_{1:t})}
$$

对上式进行以下化简：

每帧激光数据独立， $z_i$ 之间相互不关联
每帧激光数据只与该一时刻位姿相关，即 $z_i$ 只与 $x_i$ 只在 $i$ 相等时相关
每个栅格 $m_i$ 与每一对 $x_i$ 和 $z_i$ 同时相关，与单一项不相关（例如只有位姿没有观测）

可得（变化部分加粗表示）：

$$
p(m_i|x_{1:t}, z_{1:t}) = \frac{p(z_t|\mathbf{m_i,x_t})p(m_i|z_{1:t-1},x_{1:\mathbf{t-1}})}{p(z_t|\mathbf{x_t})}
$$

其中，

$$
p(z_t|m_i,x_t) = \frac{p(m_i|z_t,x_t)p(z_t|x_t)}{p(m_i|x_t)} = \frac{p(m_i|z_t,x_t)p(z_t|x_t)}{p(m_i)}
$$

代入得：

$$
\begin{aligned}
p(m_i|x_{1:t}, z_{1:t}) &= \frac{p(m_i|z_t,x_t)p(z_t|x_t)}{p(m_i)}\frac{p(m_i|z_{1:t-1},x_{1:t-1})}{p(z_t|x_t)} \\
&= \frac{p(m_i|z_t,x_t)p(m_i|z_{1:t-1},x_{1:t-1})}{p(m_i)}
\end{aligned}
$$

同样，由于 $m_i$ 是二值的，因此对 $\neg m_i$ 形式完全一样：

$$
\begin{aligned}
p(\neg m_i|x_{1:t}, z_{1:t}) &= \frac{p(\neg m_i|z_t,x_t)p(z_t|x_t)}{p(m_i)}\frac{p(\neg m_i|z_{1:t-1},x_{1:t-1})}{p(z_t|x_t)} \\
&= \frac{p(\neg m_i|z_t,x_t)p(\neg m_i|z_{1:t-1},x_{1:t-1})}{p(\neg m_i)}
\end{aligned}
$$

对上述两式相除有：

$$
\begin{aligned}
\frac{p(m_i|x_{1:t}, z_{1:t})}{p(\neg m_i|x_{1:t}, z_{1:t})} &= \frac{p(\neg m_i)p(m_i|z_t,x_t)p(m_i|z_{1:t-1},x_{1:t-1})}{p(m_i)p(\neg m_i|z_t,x_t)p(\neg m_i|z_{1:t-1},x_{1:t-1})}
\end{aligned}
$$

同样由于 $m_i$ 是二值的，有： $p(\neg m_i|x_{1:t}, z_{1:t}) = 1 - p(m_i|x_{1:t}, z_{1:t})$

代入比例式中：

$$
\begin{aligned}
    \frac{p(m_i|x_{1:t}, z_{1:t})}{p(\neg m_i|x_{1:t}, z_{1:t})} &= \frac{p(m_i|x_{1:t}, z_{1:t})}{1 - p(m_i|x_{1:t}, z_{1:t})} \\
    &= \frac{1- p(m_i)p(m_i|z_t,x_t)p(m_i|z_{1:t-1},x_{1:t-1})}{p(m_i) (1- p(m_i|z_t,x_t))(1 - p(m_i|z_{1:t-1},x_{1:t-1}))}
\end{aligned}
$$

在概率相乘的式子中我们经常使用取对数的技巧，因为这样可以将乘法变成加法，比较好处理，这里同样进行这么操作：

$$
\log {\frac{p(m_i|x_{1:t}, z_{1:t})}{p(\neg m_i|x_{1:t}, z_{1:t})}} = \log \frac{1- p(m_i)}{p(m_i)} + \log {\frac{p(m_i|z_t,x_t)}{1- p(m_i|z_t,x_t)} + \log {\frac{p(m_i|z_{1:t-1},x_{1:t-1})}{1 - p(m_i|z_{1:t-1},x_{1:t-1})}}}
$$

由于 $m_i$ 是二值的，所以当知道 $p(m_i)$ 时也可以计算出 $p(\neg m_i)$ ，这里为了简化，计算过程，我们定义一个中间量：

$$
l(x) = \log{\frac{p(x)}{1 - p(x)}}
$$

当知道 $l(x)$ 时，不难计算出： $p(x) = 1 - \frac{1}{1 + \exp {l(x)}}$

因此上式可以简化为：

$$
l(m_i|x_{1:t},z_{1:t}) = l(m_i|z_t,x_t) + l(m_i | z_{1:t-1},x_{1:t-1}) - l(m_i)
$$

式子中有以下几个部分：

$l(m_i)$ : 栅格 $m_i$ 的先验值，我们对所有栅格可以设定同样一个初始值
$l(m_i|z_{1:t-1},x_{1:t-1})$ :
- 在 $t - 1$ 时刻的数据时 $m_i$ 的状态
$l(m_i|z_t,x_t)$ : 传感器的逆观测模型（inverse measurement model），因为正常的观测模型为给定 $t$ 时刻的地图 $m_i$ 和位姿 $x_t$ 对 $z_t$ 的结果，而这里是反过来的

这里主要针对激光雷达的逆观测模型作说明，通常情况下有几种可能：

不经过该栅格， $l(m_i|z_t,x_t) = 0$ 不产生影响，在这一时刻不会处理这个栅格
经过栅格没受到阻拦， $l(m_i|z_t,x_t) = -a$ ，由于穿过去了，表面该位置有障碍物的可能性比较低，因此我们用负值表示， $a$ 的大小取决于我们对其的相信程度
经过栅格被阻拦了， $l(m_i|z_t,x_t) = +b$ ，和上述类似

上面的式子上如果不考虑 $l(m_i)$ （因为是常值），本质上他是一个递推式，即这个等式描述了：给定前 $1:t_1$ 的相关数据和 $t$ 时刻的数据，对地图的更新方法，因此整个算法的过程就得出来了，如下所示：

计数建图算法

基本概念

对每一个栅格 $m_i$ 统计两个量: misses(i) 和 hits(i)，其中：
- misses(i) 表示 i 栅格被通过（即被标为 free）的次数
- hits(i) 表示 i 被激光束击中（即标为 occupied）的次数
hits(i) / (misses(i) + hits(i)) 表示 i 状态的极大似然估计（下面进行证明），当其超过一定阈值时则认为该栅格为 occupied,否则为 free

激光雷达观测模型

$x_t$ ： $t$ 时刻的机器人位姿

$z_t$ ： $t$ 时刻的激光数据，可以理解为一个数组，每一束激光束的数组 $z_{t, i}$ 表示第 $i$ 个激光束最终停在该方向上第 $z_{t, i}$ 个栅格上，第 n 个激光束沿着射线方向一共穿过 $z_{t,n} - 1$ 个栅格，击中 $1$ 个栅格

$c_{t,n}$ ：表示 $t$ 时刻的第 $n$ 个激光束是否为最大值，即达到激光测距极限，此时该距离为无效值，不能表示该方向上第 $z_{t, n}$ 个栅格有障碍物， $c_{t,n} = 1$ 表示达到最大值， $c_{t,n} = 0$ 表示正常值

$f(x_t, n, z_{t,n})$ ：表示 $t$ 时刻第 $n$ 个激光束击中的栅格的下标，因此 $m_{f(x_t, n, z_{t,n})}$ 为该栅格的占用概率，通过上述的分析可以得出：

$$
p(z_{t,n}|x_t,m) = \left\{
\begin{aligned}
    &\prod_{k=0}^{z_{t,n}-1}(1 - m_{f(x_t, n, z_{t,n})}) &  c_{t,n} = 1\\
    &m_{f(x_t, n, z_{t,n})}\prod_{k=0}^{z_{t,n}-1}(1 - m_{f(x_t, n, z_{t,n})})  & c_{t,n} = 0
\end{aligned}
\right.
$$

简单来说上面的式子表示，当第 $n$ 个激光束：

返回无效（最大）距离时：在给定的位姿 $x_t$ 和地图 $m$ 的条件下，在该方向击中第 $z_{t,n}$ 个栅格的概率为：该方向前 $z_{t,n} - 1$ 个栅格都为 free 的概率，这个时候我们不用考虑最后一个栅格是否有障碍物，因为无论有没有激光束最远也只能到那个栅格
返回有效值时，除了要满足前 $z_{t,n} - 1$ 个栅格都为 free 的条件外，还必须要乘上第 $z_{t,n}$ 为 occupied 的概率，因为只有当它是 occupied 才会击中该栅格

地图估计的数学描述

由上我们可以知道要找出最符合当前位姿 $x_{1:t}$ 和观测 $z_{1:t}$ 的地图 $m$ （如下所示）：

$$
m^*=\arg\max_m P(m|x_{1:t},z_{1:t})
$$

等效于求一个 $m$ 使得在当前的 $m$ 和位姿 $x_{1:t}$ 的情况下，得到当前观测 $z_{1:t}$ 的概率，即：

$$
\begin{aligned}
    m^* &= \arg\max_m P(z_{1:t}|m,x_{1:t}) \\
        &= \arg\max_m \prod_t P(z_t|m,x_t) \\
        &\Leftrightarrow \arg\max_m\sum_t\ln{P(z_t|m,x_t)}
\end{aligned}
$$

上式中最后转变为求 $P(z_t|m,x_t)$ ，即每帧激光数据的观测模型，而通过上一部分我们已经求出了每一帧中每一束激光数据的观测模型，可以得到：

$$
\begin{aligned}
P(z_t|m,x_t) &= \prod_nP(z_{t,n}|m,x_t) \\
&= \left\{
    \begin{aligned}
        &\prod_n\prod_{k=0}^{z_{t,n}-1}(1 - m_{f(x_t, n, z_{t,n})}) &  c_{t,n} = 1\\
        &\prod_nm_{f(x_t, n, z_{t,n})}\prod_{k=0}^{z_{t,n}-1}(1 - m_{f(x_t, n, z_{t,n})})  & c_{t,n} = 0
    \end{aligned}
    \right. \\
    &= \prod_n (m_{f(x_t, n, z_{t,n})})^{c_{t,n} - 1}\prod_{k=0}^{z_{t,n}-1}(1 - m_{f(x_t, n, z_{t,n})})
\end{aligned}
$$

这里的 $m$ 可以表示任何栅格，那么当我们考虑一个栅格 $m_j$ 时，则有：

$$
\begin{aligned}
P(z_t|m_j,x_t) &= \prod_nP(z_{t,n}|m_j,x_t) \\
    \ln P(z_t|m_j,x_t)&= \ln\sum_n(I(f(x_t, n, z_{t,n}) = j)(1 - c_{t,n})\ln m_j + \sum_{k=0}^{z_{t,n}-1}I(f(x_t, n, z_{t,n}) = j)(1 - m_j))
\end{aligned}
$$

其中，

$$
I(x = y) = \left\{
    \begin{aligned}
        1 && x = y \\
        0 && x \neq y
    \end{aligned}
    \right.
$$

我们用 $I(f(x_t, n, z_{t,n}) = j)$ 来筛选出击中栅格 $m_j$ 的激光束，用 $(1 - c_{t,n})$ 来区分是否为有效值

因此地图估计的数学表达可以转换为：

$$
\begin{aligned}
    m^* &= \arg\max_m\sum_t\ln{P(z_t|m,x_t)} \\
    &= \arg\max_m\sum_j\sum_t\sum_n(I(f(x_t, n, z_{t,n}) = j)(1 - c_{t,n})\ln m_j +\\
        &\qquad\qquad\qquad\qquad \qquad \sum_{k=0}^{z_{t,n}-1}I(f(x_t, n, z_{t,n}) = j)(1 - m_j))
\end{aligned}
$$

其中，

$\sum_t$ 表示遍历所有激光帧（时刻）
$\sum_j$ 表示遍历所有栅格位置
$\sum_n$ 表示遍历一个激光帧的所有激光束

对上式中的两项，我们分别来看

$ $a_j = \sum_t^T\sum_n^N(I(f(x_t, n, z_{t,n}) = j)(1 - c_{t,n})$ $
- 这表示了所有激光帧中所有激光束正常击中（不是在极限距离） $m_j$ 栅格的次数 $hits(j)$
$ $b_j = \sum_t^T\sum_n^N\sum_{k=0}^{z_{t,n}-1}I(f(x_t, n, z_{t,n}) = j)$ $
- 表示栅格 $m_j$ 被所有激光帧中所有激光束穿过的次数 $miss(j)$

则上述式子变成：

$$
m^* = \arg\max_m\sum_j^Ja_j\ln{m_j} + b_j\ln{(1-m_j)} = \arg\max_m\sum_j^JF(m_j)
$$

$F(m_j)$ 是个简单函数，可以直接对其求导且令导数为 0：

$$
\begin{aligned}
    \frac{\partial F(m_j)}{\partial m_j} &= \frac{a_j}{m_j} - \frac{b_j}{1-m_j} = 0 \\
    &\Rightarrow m_j = \frac{a_j}{a_j + b_j}
\end{aligned}
$$

因此可以得到我们最开始的结论：hits(i) / (misses(i) + hits(i)) 表示 i 状态的极大似然估计

TSDF（Truncated signed distance function）建图算法

基本思想

考虑传感器测量的不确定性，利用多次测量数据来实现更为精确的表面重构，从而使得地图更精确、障碍物（墙壁）更细、更薄
为障碍物表面建立 Signed Distance Function （有符号距离函数）
考虑到距离表面较远的点不会影响到表面重构，对其忽略不计

TSDF

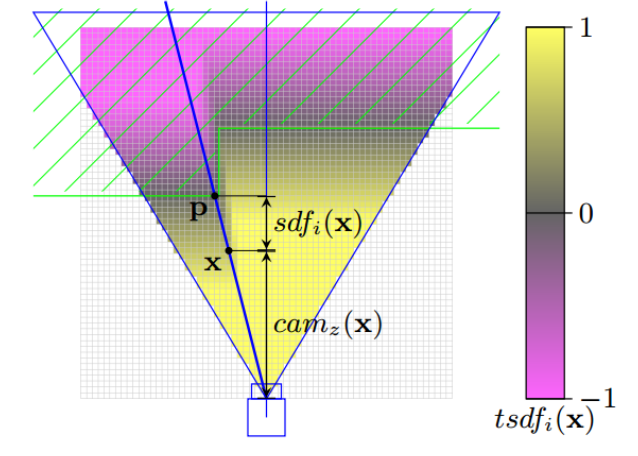
首先介绍一下 $sdf(x)$ 函数定义：

$$
sdf_i(x) = \mathrm{laser}_i(x) - \mathrm{dist}_i(x)
$$

其中：

$\mathrm{laser}_i(x)$ 表示激光测量距离
$\mathrm{dist}_i(x)$ 表示栅格离传感器原点的距离

而 $\mathrm{tsdf}(x)$ 则是在 $sdf(x)$ 进行截断，限制大小在 $[-1, 1]$ 之内：

$$
\mathrm{tsdf}_i(x) = \max(-1, \min(1, \frac{sdf_i(x)}{t}))
$$

通过这个方法我们可以得到一个栅格场，场中每个值都在 $[-1, 1]$ 之间，通过 $sdf_i(x)$ 的定义我们可以发现激光束击中附近的区域场值会趋近于 0，我们认为场值为 0 的位置是障碍物。并且由于场值是通过插值来计算的，所以可以想象不会有很厚的墙壁（只要栅格距离稍微远离差值就会变大），因此达到精确构建障碍物的效果

栅格的更新方法为（多个观测融合）：

$$
\begin{aligned}
\mathrm{tsdf}_i(\mathbf{x})&=\frac{W_{i-1}(\mathbf{x})\mathrm{tsdf}_{I-1}(\mathbf{x})+\omega_i(\mathbf{x}\mathrm{tsdf}_i(\mathbf{x}))}{W_{i-1}(\mathbf{x})+\omega_i(\mathbf{x})} \\
W_i(\mathbf{x}) &= W_{i-1}(\mathbf{x}) + \omega_i(\mathbf{x})
\end{aligned}
$$

上式其实是一个迭代形式的加权最小二乘解，通过不断按照上式融合观测值，可以构造出整个地图的 \mathrm{tsdf} 场，并插值求出障碍物曲面

TSDF 实例

假设机器人位置为 $(0, 0)$ ，障碍物位置在 $(10, 0)$ 。地图分辨率为 0.05, 截断距离为 0.1（考虑精度为0.1以内的栅格）对障碍物进行 5 次测量，测量值分别为：9.9494,10.0178,9.9733,10.0068,9.9676，如图所示：

在计算出更新后的每个栅格 TSDF 后，如果将 TSDF = 0 作为障碍物标准，则可以推断其在 cell2 和 cell3 之间，我们令 $b = sdf(cell2) = 0.03298, a = sdf(cell3) = -0.010702$ 通过线性插值可以求出：

$$
x = 9.95 - 0.05\frac{b}{a - b} = 9.9830
$$

假如我们直接对五次观测数据求加权平均有：

$$
x' = \frac{9.9494 + 10.0178 + 9.9733 + 10.0068 + 9.9676}{5} = 9.9830
$$

所以本质上 TSDF 的过程就是对观测结果求加权最小二乘解，因此我们可以知道只有在传感器噪声服从高斯分布时，通过 TSDF 进行融合才能得到比较好的结果

TSDF 算法

寻找 TSDF 场中符号进行变化的栅格，进曲面所在位置
在该两个栅格之间进行插值，插值得到 0 的坐标就是曲面精确位置
融合多帧观测，也相当于对多帧观测数据进行加权最小二乘求解
由于我们是通过插值得到障碍区曲面，所以构建的地图最多只有一个栅格厚度