[论文阅读]LiDAR Inertial Odometry Aided Robust LiDAR Localization System in Changing City Scenes

简介

论文地址见：LiDAR Inertial Odometry Aided Robust LiDAR Localization System in Changing City Scenes

在这篇论文里面，作者将一个 LIO 模块和基于匹配的全局定位模块使用图优化框架结合起来。利用地图匹配和帧间里程计互补可以在地图有一些错误或者失效时也能够达到较为稳定的定位效果。

如上图所示，图 A 和 B 反映了同一地点在两个时间内的变化。图 C 表示在错误地图下仍然有比较好的定位表现，图 D 和 E 反映了检测地图变动以及重新更新地图的过程。

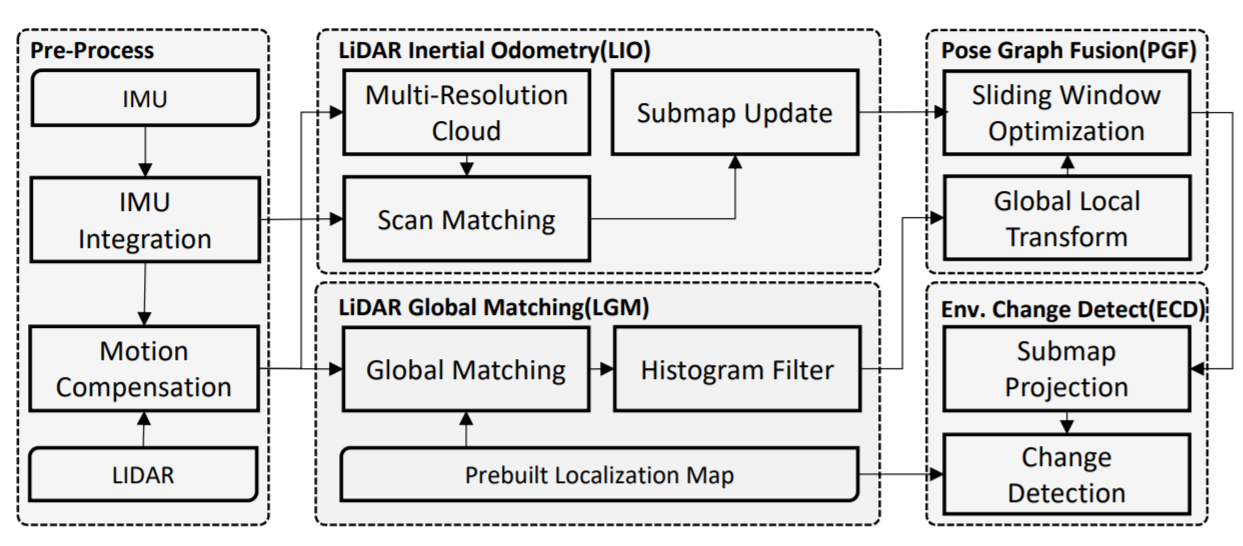
系统总览

论文中提出的算法框架如下：

主要分为五个模块：

数据预处理：主要进行 IMU 积分对点云进行运动补偿
LIO：帧间里程计
Lidar Global Matching(LGM)：基于先验地图进行全局匹配
Pose Graph Fusion (PGF)：接收 LIO 和 LGM 的位姿估计结果进行位姿图优化
Environment Change Detection(ECD)：环境变动检测

上述模块中，关于 LGM 作者使用的是他们之前另一篇论文中提出的算法：Robust and Precise Vehicle Localization based on Multi-sensor Fusion in Diverse City Scenes。LGM 模块能够通过水平匹配获得车辆的 x, y, yaw。至于其他三个自由度 altitude, roll, pitch 则有 IMU 的重力测量值得到。

整篇论文要求解的是在一个滑动窗口内的最大后验概率估计问题。涉及到的变量如下：

$\mathcal{X} = \{\boldsymbol{x}_k\}$ 滑动窗口内的状态
$\mathcal{Z} = \{\boldsymbol{z}_k\}$ 滑动窗口内的观测
$\boldsymbol{x}_k = [\boldsymbol{\omega}_k, \boldsymbol{t}_k, \boldsymbol{v}_k, \boldsymbol{b}_k]$ ，状态包括每个时刻内的位姿、速度以及 IMU 零偏。位姿用李代数 $\boldsymbol{\omega}_k$ 表示，其旋转矩阵为 $\boldsymbol{R}_k = \exp{(\boldsymbol{\omega}_k)}$ 。
$\boldsymbol{b}_k = [\boldsymbol{b}^a_k, \boldsymbol{\omega}^g_k]$ 。IMU 零偏包括加速度计零偏和陀螺仪零偏

Lidar Inertial Odometry

LIO 这部分作者基于 Cartographer 的模块进行了一定扩展。关于 Cartographer 的原理可以参考：Real-time loop closure in 2D LiDAR SLAM。作者的拓展主要在以下几点：

使用 3D 占据栅格模型来获得 6 自由度位姿
使用了 IMU 来提供帧间运动初值并且可以对点云进行运动补偿去畸变，在使用 IMU 时，为了控制运算规模，采用了预积分方法
对于占据栅格地图的栅格值，除了考虑占据概率以外，还将 Lidar 的反射值也考虑在内，这样对路面标志的识别效果更好
建立多分辨率的地图使得求解非线性优化问题时能够有一种 Coarse-To-Fine 的效果。

论文中将 LIO 问题建模为最大后验概率估计问题，也是一种常见的做法。 $k$ 时刻的状态后验估计如下所示：

$$
P(\boldsymbol{x}_k^L|\boldsymbol{z}_{k-1}^L, \mathcal{S})\propto P(\boldsymbol{z}_k^P|\boldsymbol{x}_k^L, \mathcal{S}_{k-1})P(\boldsymbol{z}_k^I|\boldsymbol{x}_k^L, \boldsymbol{x}_{k-1}^L)
$$

上式中，观测包括两部分： $\boldsymbol{z}_k^P$ 和 $\boldsymbol{z}_k^I$ 分别表示点云观测和 IMU 观测。状态 $\boldsymbol{x}^L$ 中的上标表示在局部子图中的位姿。基于高斯分布构建 IMU 和点云观测的残差：

$$
\begin{aligned}
P(\boldsymbol{z}_k^P|\boldsymbol{x}_k^L, \mathcal{S}_{k-1}) &\propto\prod_{i}\prod_{j}\exp{\frac{1}{2\sigma_{O_i}}||\text{SSOP}||^2}\prod_{i}\prod_{j}\exp{\frac{1}{2\sigma_{r_i}}||\text{SSID}||^2}\\
P(\boldsymbol{z}_k^I|\boldsymbol{x}_k^L, \boldsymbol{x}_{k-1}^L) &\propto\frac{1}{2}||\boldsymbol{r}_k^I||^2_{\Lambda^I_k}
\end{aligned}
$$

上式中 $P(\boldsymbol{z}_k^I|\boldsymbol{x}_k^L, \boldsymbol{x}_{k-1}^L)$ 描述了 IMU 观测值的残差，这里论文使用 IMU 预积分作为观测。关于预积分及其残差构建可以参考On-Manifold Preintegration for Real-Time Visual-Inertial Odometry 也可以参考我之前整理的：VIO 残差函数的构建。下面主要介绍一下点云残差的计算。上式中 SSOP 表示 Sum of Squared Occupancy Probablity 即栅格占据概率平方和，SSID 表示 Sum of Squared Intensity Difference 即反射值差异平方和。

对于一个帧点云中的任意一个激光点，在分辨率为 $i$ 的子图下，这两个残差的计算方式如下：

$$
\begin{aligned}
\text{SSOP} &= 1 - P(s)\\
\text{SSID} &= \frac{\mu_s - I(\boldsymbol{p}_j)}{\sigma_s}
\end{aligned}
$$

其中 $P(s)$ 表示该雷达点集中的栅格被占据的概率。该栅格的占据概率基本按照 Cartographer 原来的算法使用对数概率表示和二值贝叶斯滤波进行更新。以此，该栅格被占据的概率更大，SSOP 越低，表示位姿预测值越准确。 $I(\boldsymbol{p}_j)$ 表示该点的反射值， $\mu_s$ 和 $\sigma_s$ 表示该点集中栅格的反射值均值和方差。 $\sigma_{O_i}$ 和 $\sigma_{I_i}$ 分别作为占据概率和反射值的权重参数在不同分辨率的子图中会相应改变。

通过高斯分布建模的方式最后可以将问题转变为最小二乘问题，使用非线性优化的方式求解。常见的库有 Ceres, G2O，优化方法为高斯牛顿和 LM 法等。

Pose Graph Fusion

上一部分中介绍的 LIO 部分可以在局部地图中提供比较好的约束（起到里程计的作用），但是除此之外我们需要全局约束来提供全局准确性。LGM 模块能够提供这一点。关于 LGM 模块作者主要使用他们直接提出的框架，可以参考：Robust and Precise Vehicle Localization based on Multi-sensor Fusion in Diverse City Scenes。在获得了全局约束之后，需要将这两种约束同放入位姿图中进行融合，这就是 PGF 这一部分的内容。首先还是将问题建模成 MAP 问题如下所示：

$$
P(\mathcal{X}|\mathcal{Z}) \propto\prod_{k, s}P(\boldsymbol{z}_{ks}^O|\boldsymbol{x}^L_k, \boldsymbol{x}^S_s)\prod_kP(\boldsymbol{z}_k^I|\boldsymbol{x}^L_k, \boldsymbol{x}^L_{k-1})\prod_kP(\boldsymbol{z}^G_k|\boldsymbol{x}_k^L,\boldsymbol{x}_L^T)
$$

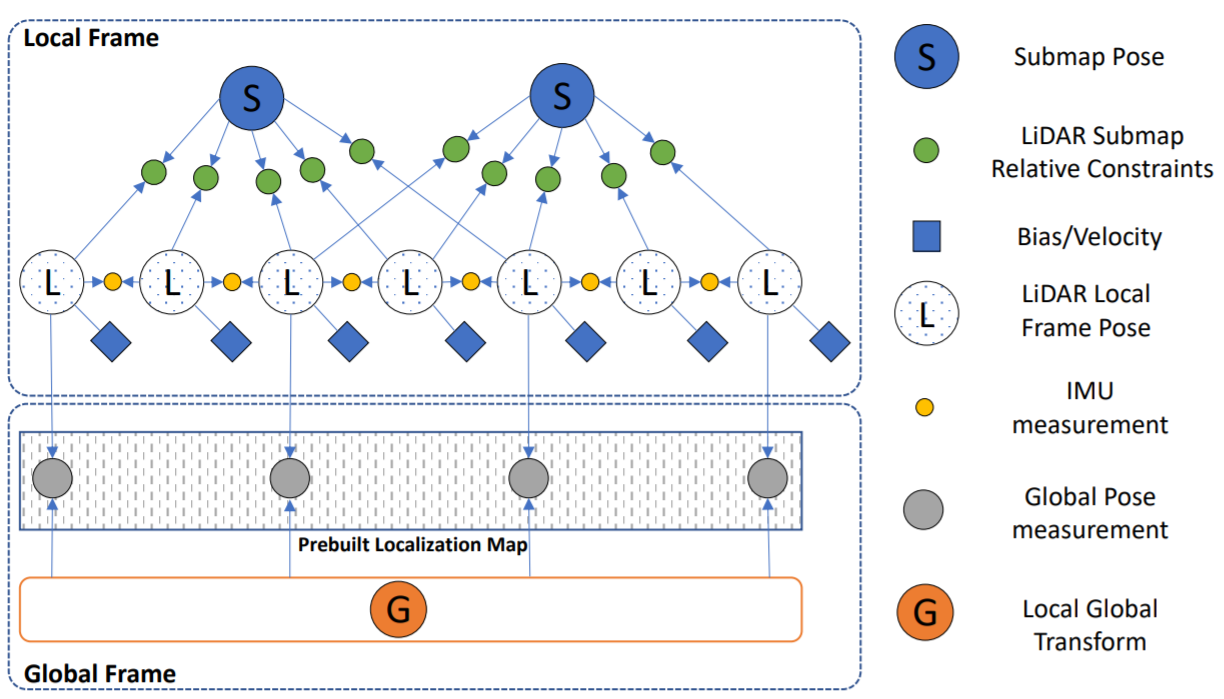
对应的贝叶斯网络如下图所示：

基于高斯分布假设，将 MAP 问题转换至最小二乘问题，各个观测的残差可以用以下二范数来表示：

$$
\begin{aligned}
P(\boldsymbol{z}_{ks}^O|\boldsymbol{x}^L_k, \boldsymbol{x}^S_s) &= \exp{-\frac{1}{2}||\boldsymbol{r}^O_{ks}||^2_{\Lambda^O}}\\
P(\boldsymbol{z}_k^I|\boldsymbol{x}^L_k, \boldsymbol{x}^L_{k-1}) &= \exp{-\frac{1}{2}||\boldsymbol{r}^I_k||^2_{\Lambda^I_k}}\\
P(\boldsymbol{z}^G_k|\boldsymbol{x}_k^L,\boldsymbol{x}_L^T) &= \exp{-\frac{1}{2}||\boldsymbol{r}^G_k||^2_{\Lambda^G_k}}
\end{aligned}
$$

上述三个残差 $\boldsymbol{r}^O_{ks}, \boldsymbol{r}^I_k, \boldsymbol{r}^G_k$ 分别对应里程计、惯性以及全局约束。在作者的融合框架，主要维护以下两个状态：

局部坐标系下的状态： $\boldsymbol{x}_k^L$
全局坐标系下的状态： $\boldsymbol{x}^G_L$ ，可以将局部位姿转换至全局位姿

假设局部状态： $\boldsymbol{x}_k^L = [\boldsymbol{R}^L_k, \boldsymbol{t}^L_k]$ ，全局状态为： $\boldsymbol{x}^G_L=[\boldsymbol{R}^G_L, \boldsymbol{t}^G_L]$ 。而全局状态的测量值为： $\boldsymbol{z}^G_k = [\boldsymbol{R}^G_k, \boldsymbol{t}^G_k]$ 。定义全局残差为： $(\boldsymbol{r}^G_k)^T = [\log{\boldsymbol{(\boldsymbol{R}_{rG})}^T}, \boldsymbol{t}_{rG}^T]$ 。 $\log{()}$ 表示对旋转矩阵求对应的李代数。残差的计算方式为：

$$
\begin{aligned}
\begin{bmatrix}
    \boldsymbol{R}_{rG} & \boldsymbol{t}_{rG}\\
    \boldsymbol{0} & 1
\end{bmatrix} &= (\boldsymbol{z}^G_k)^{-1}(\boldsymbol{x}^G_L\boldsymbol{x}_k^L)\\
&=
\begin{bmatrix}
    \boldsymbol{R}_{k}^G & \boldsymbol{t}_{k}^G\\
    \boldsymbol{0} & 1
\end{bmatrix}^{-1}
\begin{bmatrix}
    \boldsymbol{R}_{L}^G & \boldsymbol{t}_{L}^G\\
    \boldsymbol{0} & 1
\end{bmatrix}
\begin{bmatrix}
    \boldsymbol{R}_{k}^L & \boldsymbol{t}_{k}^L\\
    \boldsymbol{0} & 1
\end{bmatrix}
\end{aligned}
$$

对应的的协方差矩阵定义为： $\boldsymbol{\Lambda}^G_k = \text{diag}(\Lambda^{G_\omega}, \Lambda^{G_h}, \Lambda^{G_z})$ 。可以看到总共由三部分组成，分别介绍如下：

$\Lambda^{G_\omega}\in\mathbb{R}^{3\times 3}$ ：常值对角矩阵，因为 LGM 只进行水平定位所以没办法确定姿态不确定度
$\Lambda^{G_z}\in\mathbb{R}^{1\times1}$ ：常值矩阵，因为 LGM 不进行高度方向上的定位
$\Lambda^{G_h}\in\mathbb{R}^{2\times2}$ ：在每一个时刻由 LGM 模块进行计算

考虑到里程计残差计算规模，子图会不断进行迭代。子图和局部坐标系之间的相对位姿会通过一个滑动窗口维护。如果将子图下的位姿定义为： $\boldsymbol{x}_s^S = [\boldsymbol{R}^S_s, \boldsymbol{t}^S_s]$ ，子图和局部坐标系之间的相对约束为： $\boldsymbol{x}_{ks}^O = [\boldsymbol{R}_{ks}^O, \boldsymbol{t}_{ks}^O]$ ，残差定义为： $(\boldsymbol{r}_{ks}^O)^T = [\log{\boldsymbol{(\boldsymbol{R}_{rO})}^T}, \boldsymbol{t}_{rO}^T]$ 。则有：

$$
\begin{aligned}
\begin{bmatrix}
    \boldsymbol{R}_{rO} & \boldsymbol{t}_{rO}\\
    \boldsymbol{0} & 1
\end{bmatrix} &= (\boldsymbol{z}_{ks}^O)^{-1}(\boldsymbol{x}^S_s\boldsymbol{x}_k^L)\\
&=
\begin{bmatrix}
    \boldsymbol{R}_{ks}^O & \boldsymbol{t}_{ks}^O\\
    \boldsymbol{0} & 1
\end{bmatrix}^{-1}
\begin{bmatrix}
    \boldsymbol{R}_{s}^S & \boldsymbol{t}_{s}^S\\
    \boldsymbol{0} & 1
\end{bmatrix}
\begin{bmatrix}
    \boldsymbol{R}_{k}^L & \boldsymbol{t}_{k}^L\\
    \boldsymbol{0} & 1
\end{bmatrix}
\end{aligned}
$$

对应这部分残差的协方差矩阵作为用一个常值对角阵来表示，即所有帧和子图之间的相对估计不确定度视为一样的。

预积分的协方差矩阵可以通过单个测量的不确定度（IMU 的随机误差）并计算扩散得到，具体过程可以参考：VIO 残差函数的构建

Envionmental Change Detection

LGM 提供的基于先验地图的定位需要依赖先验地图的实时性，即从建图时间到当前时间地图不能发生太大变化。LIO 模块不仅能够提供帧与帧之间的相对位姿约束，还能够用来检测地图变动。这里，作者团队基于 LIO 中维护的子图建立一个环境变动检测模块。其工作原理如下：

将 3D 多分辨率子图投影到地面平面，获得和 LGM 中使用的地图类似的投影子图。
基于定位结果可以将子图 $\mathcal{S}$ 和先验地图 $\mathcal{M}$ 进行重叠。
进行栅格之间 (cell by cell) 之间的比较来判断环境是否有变化。

作者使用的栅格比较的方法主要是基于每个栅格的高度值和反射值。设子图中某一栅格的反射值的均值和方差为： $\mu_s, \sigma_s$ ，高度度值为 $a_s$ 。地图中对应的栅格的反射值的均值和方差以及高度值为： $\mu_m, \sigma_m, a_m$ 。环境变动参数定义如下：

$$
\begin{aligned}
    z_s(r) &= \frac{(\mu_s-\mu_m)^2(\sigma_s^2 + \sigma_m^2)}{\sigma^2_s\sigma^2_m}\\
    z_s(a) &= (a_s - a_m)^2
\end{aligned}
$$

上述两个参数用来评估该栅格有多大可能已经发生变化。上述情况是对某一帧进行判断，而在一个子图中，我们通常会有多帧观测，因此下面作者介绍了多帧点云时如何对概率进行更新。和占据栅格的概率更新方式类似，作者基于二值贝叶斯滤波采用一个二值化的状态估计来对每个栅格的变动概率进行建模。将每个栅格的变动定义为一个二值状态 $d_s$ 。二值贝叶斯滤波的逆观测模型可以定义为：

$$
P(d_s|z_s) = \eta P(d_s|z_s(r))^{\gamma}P(d_s|z_s(a))^{1-\gamma}
$$

上式中， $\gamma$ 作为反射值和高度值之间的权重调节系数。对其中涉及的两个概率可以进一步定位以下形式：

$$
\left\{
\begin{aligned}
    P^{-1}(d_s|z_s(r)) &= 1 + \exp{(-\beta_1(\frac{z_s(r)-\mu_s(r)}{\sigma_s(r)}- \theta_1))}\\
    P^{-1}(d_s|z_s(a)) &= 1 + \exp{(-\beta_2(\frac{z_s(a)-\mu_s(a)}{\sigma_s(a)}- \theta_2))}
\end{aligned}
\right.
$$

上式中， $\mu_s(r), \sigma_s(r), \mu_s(a), \sigma_s(a)$ 分别是多帧观测中 $z_s(r), z_s(a)$ 的均值和方差。 $\beta, \theta$ 是外部调节参数。

实验

TODO

结论

TODO