简介

LINS 提出一种框架融合 IMU 和 Lidar 信息对无人机的实时姿态进行估计。LINS 的特点有：

• 实现了雷达和惯性里程计的紧耦合，相比于 LIO-Mapping 速度提升了一个数量级
• 提出了一种以机器人为中心的迭代 ESKF 算法，并通过各种场景验证其可行性
• 代码开源（参考了 LOAM 和 LeGO-LOAM 的代码）

相关工作

下面列举一些相关工作。

纯雷达方法：

• LOAM
• LeGO-LOAM

Lidar 和 IMU 进行松耦合方法

• IMU-aided LOAM：原始的 LOAM 代码中有提供利用 IMU 进行相对位姿初始化的功能

Lidar 和 IMU 进行紧耦合方法

• LIPS - Lips: Lidarinertial 3d plane slam
• LIO-Mapping

激光惯性融合里程计和建图

系统总览

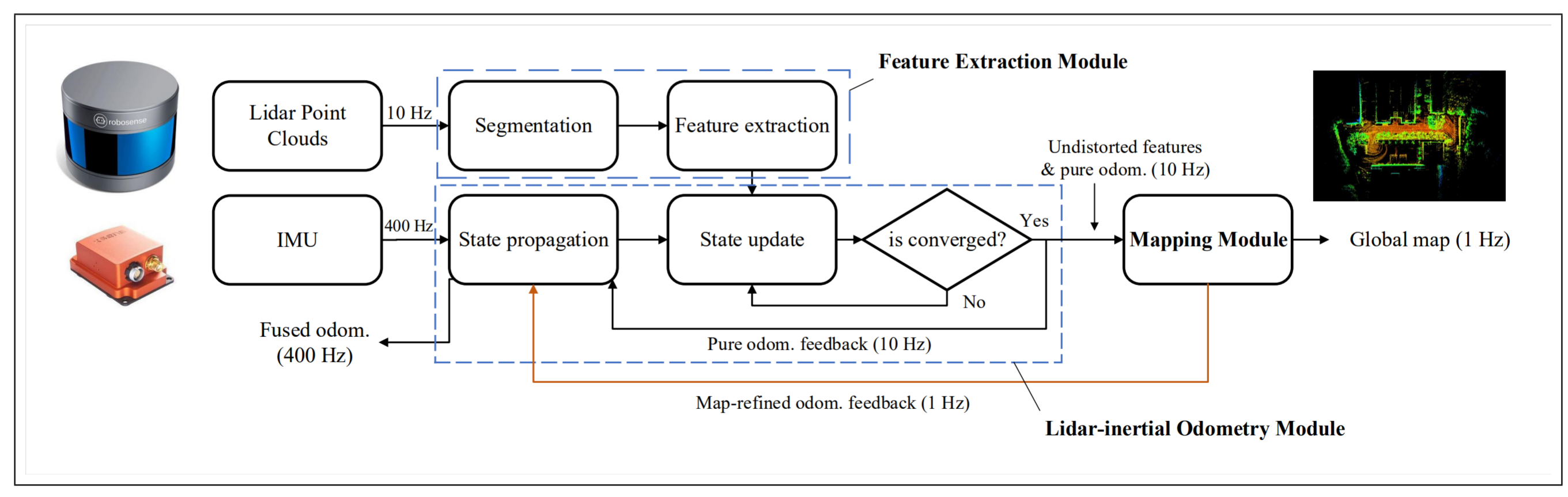
框架整体如下所示：

整体分为三个部分：

• 特征提取：从原始点云中提取稳定的特征
• 激光惯性里程计：对状态进行预测并使用迭代卡尔曼滤波进行更新
• 建图：对初始的位姿估计进行修正，并将新的特征更新至全局地图中

特征提取

特征提取部分基本和 LeGO-LOAM 和 LOAM 一致，可以参考之前我对这两个框架的整理：

• LOAM 论文阅读笔记
• LeGO-LOAM 论文阅读笔记

通过特征提取主要是将点云中的平面点（LeGO-LOAM 关注的平面点为地面点）和边缘点特征进行提取。

使用迭代 ESKF 融合 Lidar 和 IMU 信息进行状态估计

LIO 模块主要将相邻两关键帧提取的点云特征，以及这两帧点云之间的 IMU 测量信息进行融合，估计载体的相对位姿变换。融合过程中主要涉及以下几个坐标系：

• $W$：世界坐标系
• $b_k$：k 时刻的 IMU 坐标系（下面也会称为载体系）
• $l_k$：k 时刻的 Lidar 坐标系

在前后两帧点云匹配时，局部坐标系被设为上一帧点云对应时刻的 IMU 坐标系。

系统状态以及优化变量

论文中关注相邻两帧的以下状态：

$$
\begin{aligned}
    \boldsymbol{x}^{b_k}_w :&= \begin{bmatrix}\boldsymbol{p}^{b_k}_w & \boldsymbol{q}^{b_k}_{w}  \end{bmatrix}\\
    \boldsymbol{x}^{b_{k}}_{b_{k+1}} &:= 
    \begin{bmatrix}
        \boldsymbol{p}^{b_k}_{b_{k+1}}&
        \boldsymbol{v}^{b_k}_{b_{k+1}}&
        \boldsymbol{q}^{b_k}_{b_{k+1}}&
        \boldsymbol{b}_{a}&
        \boldsymbol{b}_{g}&
        \boldsymbol{g}^{b_k}
    \end{bmatrix}
\end{aligned}
$$

这里论文关注的是，上一帧的位姿(包括位置和姿态)，以及从当前到上帧的相对变换作为局部状态，包括：平移和旋转、加速度计和陀螺仪的零偏、以及载体坐标系下的重力加速度。论文中使用基于误差状态的卡尔曼滤波来对局部状态进行估计。

根据 ESKF 的思想，局部状态 $\boldsymbol{x}^{b_k}_{b_{k+1}}$ 可以分为两部分：先验 ${}^{-}\boldsymbol{x}^{b_k}_{b_{k+1}}$ 以及误差 $\delta\boldsymbol{x}$，因此定义局部状态 $\boldsymbol{x}^{b_k}_{b_{k+1}}$ 的误差向量如下所示：

$$
\delta\boldsymbol{x} = \begin{bmatrix}
    \delta\boldsymbol{p} &
    \delta\boldsymbol{v} &
    \delta\boldsymbol{\theta} &
    \delta\boldsymbol{b}_a &
    \delta\boldsymbol{b}_g &
    \delta\boldsymbol{g}
\end{bmatrix}
$$

每一次对误差向量进行估计后，通过以下方式对先验估计进行修正：

$$
\begin{aligned}
\boldsymbol{x}^{b_k}_{b_{k+1}} &= {}^{-}\boldsymbol{x}^{b_k}_{b_{k+1}} \boxplus \delta\boldsymbol{x}
    &=\begin{bmatrix}
        {}^{-}\boldsymbol{p}^{b_k}_{b_{k+1}} + \delta\boldsymbol{p}\\
        {}^{-}\boldsymbol{v}^{b_k}_{b_{k+1}} + \delta\boldsymbol{v}\\
        {}^{-}\boldsymbol{q}^{b_k}_{b_{k+1}} \otimes \exp{(\delta\boldsymbol{\theta})}\\
        {}^{-}\boldsymbol{b}_{a} + \delta\boldsymbol{b}_a\\
        {}^{-}\boldsymbol{b}_{g} + \delta\boldsymbol{b}_g\\
        {}^{-}\boldsymbol{g}^{b_k} + \delta\boldsymbol{g}
    \end{bmatrix}
\end{aligned}
$$

其中，除了四元数的更新以外其他变量的更新都是普通的矩阵加法，四元数的更新首先将旋转向量的变化量（角增量）通过指数映射转换为四元数，如下所示：

$$
\begin{aligned}
    \exp{\boldsymbol{\psi}} &= (\boldsymbol{q}_0, \check{\boldsymbol{q}}) = 
        \begin{bmatrix}
        \cos{(||\boldsymbol{\psi}||/2)} & \sin{(||\boldsymbol{\psi}||/2)\frac{\boldsymbol{\psi}}{||\boldsymbol{\psi}||}}
        \end{bmatrix}\\
            &\approx\begin{bmatrix}
            1 & \boldsymbol{\psi} /2
        \end{bmatrix} \qquad ||\boldsymbol{\psi}||\approx0
\end{aligned}
$$

这里由于误差量通常接近 0，因此用近似的方式可以很简单将角增量映射至四元数，然后通过四元数的乘法即可完成更新。

误差状态传播

首先考虑连续时间下的误差传播模型（运动模型），误差传播模型如下所示,推导过程可以参考 基于 IMU 的惯性导航解算及误差分析：

$$
\begin{aligned}
    \delta\dot{\boldsymbol{p}} &= \delta\boldsymbol{v}\\
    \dot{\delta\boldsymbol{v}}&=\boldsymbol{R}^{b_k}_t(\boldsymbol{n}_a -  \delta\boldsymbol{b}^a) -\boldsymbol{R}^{b_k}_t(\boldsymbol{a}_{m_t} - \boldsymbol{b}_a)^\wedge\delta\boldsymbol{\theta}- \delta\boldsymbol{g}^w\\
        \delta\dot{\boldsymbol{\theta}}&= -(\boldsymbol{\omega}_{m_t} - \boldsymbol{b}_g)^\wedge\delta\boldsymbol{\theta} + \boldsymbol{n}_g -  \delta\boldsymbol{b}_g\\
    \delta\dot{\boldsymbol{b}}_a &= \boldsymbol{n}_{b_a}\\
    \delta\dot{\boldsymbol{b}}_g &= \boldsymbol{n}_{b_g}\\
    \delta\dot{\boldsymbol{g}}^w &= \boldsymbol{0}
\end{aligned}
$$

上式中，$\boldsymbol{R}^{b_k}_t$ 为 t 时刻 IMU 系到 $b_k$ 对应时刻 IMU 系的旋转，$\boldsymbol{\omega}_{m_t}, \boldsymbol{a}_{m_t}$ 分别为 t 时刻 IMU 加速度计和陀螺仪的原始测量值。除此之外，上式中考虑的噪声有：加速度计和陀螺仪的测量白噪声（作用在加速度计和陀螺仪的测量值上）以及加速度计和陀螺仪的随机游走（左右在加速度计和陀螺仪的零偏上），即 $\boldsymbol{w} = [\boldsymbol{n}_a, \boldsymbol{n}_g, \boldsymbol{n}_{b_a}, \boldsymbol{n}_{b_g}]$。将上式中的状态值和噪声区分开，有：

$$
\delta\dot{\boldsymbol{x}} = \boldsymbol{F}_t\delta\boldsymbol{x} + \boldsymbol{G}_t\boldsymbol{w}_t
$$

其中，

$$
\begin{aligned}
    \boldsymbol{F}_t &= \begin{bmatrix}
        \boldsymbol{0} & \boldsymbol{I} & \boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0} \\
        \boldsymbol{0} & \boldsymbol{0} & -\boldsymbol{R}^{b_k}_t(\boldsymbol{a}_{m_t} - \boldsymbol{b}_a)^\wedge &-\boldsymbol{R}^{b_k}_t &\boldsymbol{0} & -\boldsymbol{I} \\
        \boldsymbol{0} & \boldsymbol{0} & -(\boldsymbol{\omega}_{m_t} - \boldsymbol{b}_g)^\wedge &\boldsymbol{0} &-\boldsymbol{I} &\boldsymbol{0} \\
        \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0} \\
        \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0} \\
        \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0}
    \end{bmatrix}\\
    \boldsymbol{G}_t &= \begin{bmatrix}
        \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} \\
        \boldsymbol{R}^{b_k}_t & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} \\
        \boldsymbol{0} & \boldsymbol{I} & \boldsymbol{0} & \boldsymbol{0} \\
        \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{I} & \boldsymbol{0} \\
        \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{I} \\
        \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} \\
    \end{bmatrix}
\end{aligned}
$$

这里我的推导结果和作者有点不一样，不确定是哪里有问题，但是至少作者在重力加速度变化量的变量应该笔误了。

接下来对传播模型进行离散化，离散后的公式如下所示：

$$
\begin{aligned}
    \delta\boldsymbol{x}_{t_{\tau}} &= (\boldsymbol{I} + \boldsymbol{F}_{t_{\tau}}\Delta t)\delta\boldsymbol{x}_{t_{\tau - 1}}\\
    \boldsymbol{P}_{t_{\tau}} &= (\boldsymbol{I} + \boldsymbol{F}_{t_{\tau}}\Delta t)\boldsymbol{P}_{t_{\tau - 1}}(\boldsymbol{I} + \boldsymbol{F}_{t_{\tau}}\Delta t)^T + (\boldsymbol{G}_{t_{\tau}}\Delta t)\boldsymbol{Q}(\boldsymbol{G}_{t_{\tau}}\Delta t)^T
\end{aligned}
$$

上式中，$\Delta t = t_{\tau} - t_{\tau - 1}$ 是 IMU 测量采样周期，$\boldsymbol{Q}$ 是事先设定的噪声协方差。

此外还需要对 IMU 测量数据进行解算，计算出两时刻间状态相对变化的先验估计 ${}^{-}\boldsymbol{x}^{b_k}_{b_{k+1}}$，可以参考：基于 IMU 的惯性导航解算及误差分析

误差状态更新

上述误差传播过程不是新的内容，而这篇论文主要的创新点则在误差卡尔曼滤波的更新环节，这里作者采用采用了迭代卡尔曼滤波的思路，将更新环节视为一个优化问题，优化的残差为：实际的观测值和理论观测值之间的残差、以及误差状态，即求解以下问题：

$$
\arg\min_{\delta\boldsymbol{\theta}}(||\delta\boldsymbol{x}||_{\boldsymbol{P}_k^{-1}} + ||f({}^{-}\boldsymbol{x}^{b_k}_{b_{k+1}}\boxplus\delta\boldsymbol{x})||_{(\boldsymbol{J}_k\boldsymbol{M}_k\boldsymbol{J}_k^T)^{-1}}
$$

上式尝试最小化两个变量：

• $||\delta\boldsymbol{x}||_{\boldsymbol{P}_k^{-1}}$：$\delta\boldsymbol{x}$ 和先验估计之间的马氏距离，协方差为 $\delta\boldsymbol{x}$ 的协方差矩阵
• $||f({}^{-}\boldsymbol{x}^{b_k}_{b_{k+1}}\boxplus\delta\boldsymbol{x})||_{(\boldsymbol{J}_k\boldsymbol{M}_k\boldsymbol{J}_k^T)^{-1}}$ 为更新后的状态计算出的理论测量值和实际测量值的马氏距离，权重为测量噪声协方差 $\boldsymbol{M}_k$ 经由测量模型对噪声的雅可比 $\boldsymbol{J}_k$ 进行扩散。

由于这里观测是一系列特征点（包括平面特征和角点特征），因此观测模型如下所示：

$$
f_i(\boldsymbol{x}^{b_k}_{b_{k+1}}) =\left\{
\begin{aligned}
    &\frac{|(\hat{\boldsymbol{p}}^{l_k}_i-\boldsymbol{p}_a^{l_k})\times(\hat{\boldsymbol{p}}^{l_k}_i-\boldsymbol{p}_b^{l_k})|}{|\boldsymbol{p}_a^{l_k} - \boldsymbol{p}_b^{l_k}|} &\qquad\qquad \text{if} \boldsymbol{p}_i^{l_{k+1}} \in \mathbb{F}_e\\
    &\frac{|(\hat{\boldsymbol{p}}^{l_k}_i-\boldsymbol{p}_a^{l_k})^T(\boldsymbol{p}_a^{l_k}-\boldsymbol{p}_b^{l_k})\times(\boldsymbol{p}_a^{l_k}-\boldsymbol{p}_c^{l_k})|}{|(\boldsymbol{p}_a^{l_k}-\boldsymbol{p}_b^{l_k})\times(\boldsymbol{p}_a^{l_k}-\boldsymbol{p}_c^{l_k})|} &\qquad\qquad \text{if} \boldsymbol{p}_i^{l_{k+1}} \in \mathbb{F}_p\\
\end{aligned}
\right.
$$

上述模型中：

• 如果 $\boldsymbol{p}_i^{l_{k+1}}$ 是角点（边缘特征），将其利用 $\boldsymbol{x}^{b_k}_{b_{k+1}}$ 投影至上一时刻坐标系得到 $\hat{\boldsymbol{p}}^{l_k}_i$ 中并进行特征误差的计算，大致思路是计算该点到上一时刻对应边缘线（两个点 $\boldsymbol{p}_a^{l_k}, \boldsymbol{p}_b^{l_k}$ 组成）的距离
• 如果 $\boldsymbol{p}_i^{l_{k+1}}$ 是平面点（面特征），将其利用 $\boldsymbol{x}^{b_k}_{b_{k+1}}$ 投影至上一时刻坐标系得到 $\hat{\boldsymbol{p}}^{l_k}_i$ 并进行特征误差的计算，大致思路是计算该点到上一时刻对应平面（三个点 $\boldsymbol{p}_a^{l_k}, \boldsymbol{p}_b^{l_k}, \boldsymbol{p}_c^{l_k}$ 组成）的距离。特征误差计算可以参考：[论文阅读]LOAM: Lidar Odometry and Mapping in Real-time

由于坐标点是在雷达系下的，因此利用位姿相对变化进行转换时还需要引入 IMU 和雷达之间的外参（外参线下标定），转换关系如下所示：

$$
\hat{\boldsymbol{p}}^{l_k}_i = {\boldsymbol{R}^b_l}^T(\boldsymbol{R}^{b_k}_{b_{k+1}}(\boldsymbol{R}^b_l\boldsymbol{p}_i^{l_{k+1}}+ \boldsymbol{p}_l^b)+\boldsymbol{p}^{b_k}_{b_{k+1}}-\boldsymbol{p}^b_l)
$$

了解了观测误差之后，接下来就是使用卡尔曼滤波的更新环节对这两个误差进行最小化：

$$
\begin{aligned}
    \boldsymbol{K}_{k, j} &= \boldsymbol{P}_k\boldsymbol{H}^T_{k, j}(\boldsymbol{H}_{k,j}\boldsymbol{P}_k\boldsymbol{H}^T_{k, j} + \boldsymbol{J}^{k,j}\boldsymbol{M}_k\boldsymbol{J}^T_{k,j})^{-1}\\
    \Delta\boldsymbol{x}_j &= \boldsymbol{K}_{k,j}(\boldsymbol{H}_{k,j}\delta\boldsymbol{x}_j - f({}^{-}\boldsymbol{x}^{b_k}_{b_{k+1}}\boxplus\delta\boldsymbol{x}))\\
    \delta\boldsymbol{x}_{j+1} &= \delta\boldsymbol{x}_j + \Delta\boldsymbol{x}_j
\end{aligned}
$$

上面三个式子描述了误差状态的迭代更新环节，$j$ 表示当前迭代次数，$\boldsymbol{H}_{k,j}$ 为观测模型对状态的雅可比矩阵。这里作者提到，在每一次对误差向量进行更新后，都会重新提取特征来进一步减小误差，误差重新提取后再接着计算新的 $\boldsymbol{H}_{k,j}, \boldsymbol{J}^{k,j}, \boldsymbol{K}_{k, j}$。

当误差状态收敛之后，用其对先验估计进行修正得到 $\boldsymbol{x}^{b_k}_{b_{k+1}}$ 的后验估计。并以此对当前时刻点云进行去畸变。最后，使用以下测量值，进行一相邻时刻状态变化 $\boldsymbol{x}^{b_{k+1}}_{b_{k+2}}$的初始化：

$$
\boldsymbol{x}^{b_{k+1}}_{b_{k+2}} = \begin{bmatrix}
    \boldsymbol{0} & \boldsymbol{v}^{b_{k+1}}_{b_{k+1}} & \boldsymbol{q}_0 & \boldsymbol{b}_a & \boldsymbol{b}_g & \boldsymbol{g}^{b_{k+1}}
\end{bmatrix}
$$

上式中，$\boldsymbol{v}^{b_{k+1}}_{b_{k+1}}, \boldsymbol{g}^{b_{k+1}}$ 可以由当前时刻的速度/重力加速度 $\boldsymbol{v}^{b_{k}}_{b_{k+1}}, \boldsymbol{g}^{b_{k}}$和当前状态后验估计中 $\boldsymbol{R}^{b_{k+1}}_{b_k}$，同时协方差矩阵也继承下来。而相对位置和姿态误差以及相关的协方差矩阵被重置。

全局位姿更新

每当误差向量更新完成后，需要对载体的世界坐标系下的位姿进行更新，如下所示：

$$
\boldsymbol{x}^{b_{k+1}}_w =
\begin{bmatrix}
    \boldsymbol{p}^{b_{k+1}}_w\\
    \boldsymbol{q}^{b_{k+1}}_w\\
\end{bmatrix} =
\begin{bmatrix}
    \boldsymbol{R}^{b_{k+1}}_{b_k}(\boldsymbol{p}^{b_k}_w - \boldsymbol{p}^{b_k}_{b_{k+1}})\\
    \boldsymbol{q}^{b_{k+1}}_{b_k}\otimes\boldsymbol{q}^{b_k}_w
\end{bmatrix}
$$

卡尔曼滤波初始化

论文中作者对卡尔曼滤波初始化的操作有：

• 标定 IMU 加速度计的零偏以及 Lidar 和 IMU 之间的外参，陀螺仪零偏使用静置一段时间内测量值的平均值来表示
• 初始化姿态（roll 和 pitch）由移动前加速度计测量值校正后的值来计算得到
• 初始重力加速度通过使用初始的 roll 和 pitch 将导航系的重力加速度转换至局部坐标系得到

实验

TODO

结论

TODO