简介
LOAM 虽然提供了实时、低飘移的位姿估计和建图。但是其同样有几个缺点:将不同时间观测下的点云以全局体素(Voxel)格式存储作为格式,很难进行回环检测来消除累积误差,并且将位姿估计和对应的观测分开使其很难和别的传感器观测进行融合。同时,在特征丰富的环境中,体素地图会变得很稠密使得其在线处理过程的实时性会受影响。
这篇论文中提出了将激光雷达和惯性导航进行紧耦合的位姿估计和建图算法。LIO-SAM 假定传感器在做非线性运动,并使用 IMU 测量数据来对激光雷达点云进行去畸变处理,除此之外,IMU 估计的载体运动运动还作为激光雷达里程计优化的初值。然后激光雷达里程计估计的结果被反过来进行图优化,以此来估计 IMU 的偏置。除了利用全局因子图来融合激光雷达和 IMU 的观测以外,在有需要的时候还能够融合进 GPS 对位置的绝对观测,以及指南针得到的姿态观测。此外,为了限制优化的规模,采用了边缘化的思路,在估计的时候在点云观测对一个局部地图(而不是全局地图)进行匹配。
相关工作
激光里程计的实现方式典型的有两种思路:通过整个点云进行扫描匹配,如 ICP,GICP;基于特征的匹配,如平面特征、线特征等。后者通常效率更高,但是由于激光雷达扫描过程中的旋转以及载体本身的运动会造成点云的畸变。因此通常会引入其他传感器来融合使用,思路也分为两种:松耦合和紧耦合。前者如 LOAM 中使用 IMU 的观测来对点云进行去畸变,并且作为点云匹配的初值,但并没有将其加入到优化过程中,另一种松耦合的方式是采用 EKF 对多种观测进行松耦合。而近年来,紧耦合由于其能提供更高的准确性更受青睐,如 R-LINS,LIO-Mapping。
LIO-SAM
系统总览
这篇论文中定义世界坐标系为 $W$,以 IMU 坐标系作为机器人(载体)坐标系为 $B$。载体状态由以下几个变量组成:
$$
\boldsymbol{x} = \begin{bmatrix}
\boldsymbol{R}\\
\boldsymbol{p}\\
\boldsymbol{v}\\
\boldsymbol{b}
\end{bmatrix}
$$
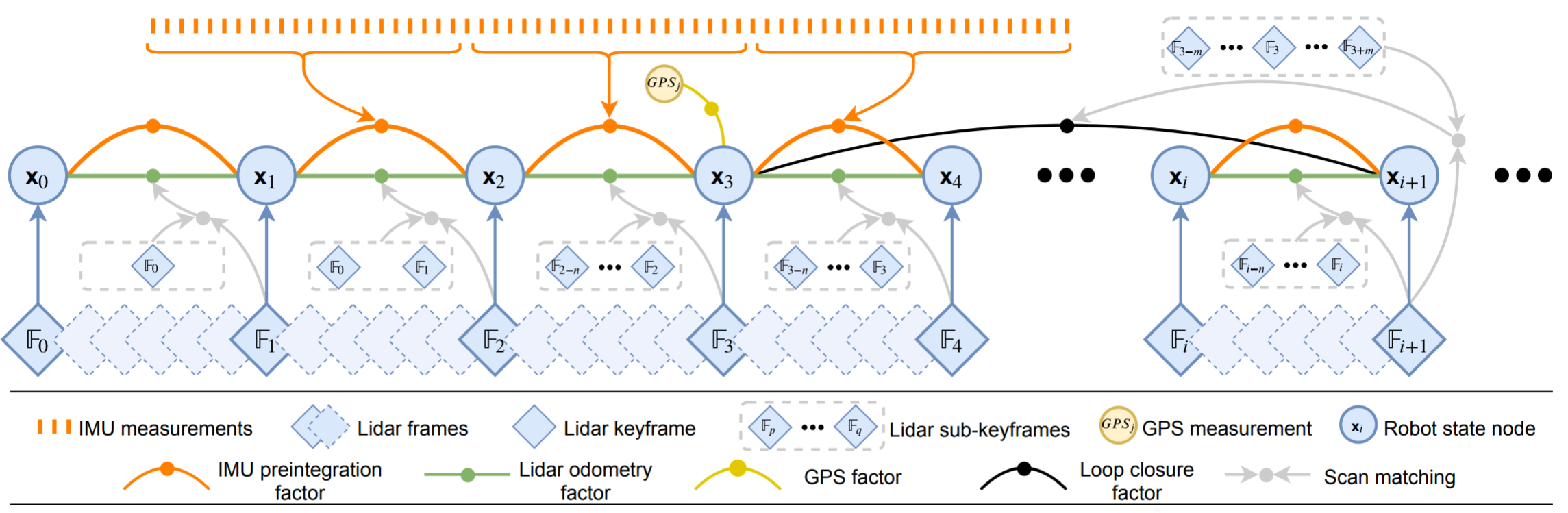
其中,$\boldsymbol{R}$ 为载体相对于世界坐标系的姿态,$\boldsymbol{p}, \boldsymbol{v}$ 分别为载体在世界坐标系中的位置和速度,$\boldsymbol{b}$ 为 IMU 的偏置。后面推导中,有时候会使用 $\boldsymbol{T} = \left[\boldsymbol{R} | \boldsymbol{p}\right]$ 作为转换矩阵表示载体在世界坐标系中的位姿。系统流程如下图所示:
LIO-SAM 要尝试解决的是对载体的位姿及其轨迹的估计问题。在这篇论文里面,这个问题被视作一个最大后验概率问题(MAP),并且构造一个因子图来对问题进行建模。基于高斯噪声的假设,这个问题可以视作一个最小二乘问题。在这个问题中,算法对一个变量融合四个因子:变量即为载体的状态,作为图中的节点,四种因子分别是:IMU 预积分因子、雷达里程计因子、GPS 因子、回环因子。每当机器人的位姿改变超过一定阈值时会将其作为一个新节点加入到图中。在新节点加入的时候,算法会对整个图使用 iSAM2 进行平滑优化以及建图。
IMU 预积分因子
论文中使用以下噪声模型对 IMU 测量值进行建模:
$$
\begin{aligned}
\tilde{\boldsymbol{\omega}}_t &= \boldsymbol{\omega}_t + \boldsymbol{b}_t^{\boldsymbol{\omega}} + \boldsymbol{n}_t^{\boldsymbol{\omega}}\\
\tilde{\boldsymbol{a}}_t &= \boldsymbol{R}^{BW}(\boldsymbol{a}_t -\boldsymbol{g}) + \boldsymbol{b}_t^{\boldsymbol{a}} + \boldsymbol{n}_t^{\boldsymbol{a}}
\end{aligned}
$$
其中,$\boldsymbol{\omega}_t$,$\boldsymbol{a}_t$ 是 IMU 的原始测量值。其中 $\boldsymbol{a}_t$ 是在参考惯性系下(论文中使用的参考惯性系是当地东北天坐标系)的加速度,因此需要转换至载体坐标系下。关于 IMU 的测量以及不同参考惯性系的选择可以参考:IMU 测量模型。基于 IMU 在离散时间下的运动解算模型如下所示:
$$
\begin{aligned}
\boldsymbol{v}_{t + \Delta t} &= \boldsymbol{v}_t + \boldsymbol{g}\Delta t + \boldsymbol{R}_t(\tilde{\boldsymbol{a}_t} + \boldsymbol{b}_t^{\boldsymbol{a}} + \boldsymbol{b}_t^{\boldsymbol{a}})\Delta t\\
\boldsymbol{p}_{t + \Delta t} &= \boldsymbol{p}_t + \boldsymbol{v}_t\Delta t + \frac{1}{2}\boldsymbol{g}\Delta t^2 + \frac{1}{2}\boldsymbol{R}(\tilde{\boldsymbol{a}}_t - \boldsymbol{b}_t^{\boldsymbol{a}} - \boldsymbol{n}_t^{\boldsymbol{a}})\Delta t^2\\
\boldsymbol{R}_{t + \Delta t} &= \boldsymbol{R}_t\exp{((\tilde{\boldsymbol{\omega}}_t - \boldsymbol{b}_t^{\boldsymbol{\omega}} - \boldsymbol{n}_t^{\boldsymbol{\omega}})\Delta t)}
\end{aligned}
$$
上式假设载体在采样时间内做加速度和角速度恒定的运动,根据 IMU 的在 $t$ 时刻的测量值与状态值解算出 $t + \Delta t$ 时刻下的状态值。接下来使用 IMU 预积分方法计算出任意两个时刻 $i, j$ 下状态量的变化值:
$$
\begin{aligned}
\Delta \boldsymbol{v}_{ij} &= \boldsymbol{R}_i^T(\boldsymbol{v}_j - \boldsymbol{v}_i + \boldsymbol{g}\Delta t_{ij})\\
\Delta \boldsymbol{p}_{ij} &= \boldsymbol{R}_i^T(\boldsymbol{p}_j - \boldsymbol{p}_i - \boldsymbol{v}_i\Delta t_{ij} - \frac{1}{2}\boldsymbol{g}\Delta t_{ij}^2)\\
\Delta\boldsymbol{R}_{ij} &= \boldsymbol{R}_i^T\boldsymbol{R}_j
\end{aligned}
$$
关于 IMU 的预积分推导部分可以参考:VIO 残差函数的构建 - IMU 预积分,利用预积分方法不仅可以节省计算不同时刻下的状态量,还能用预积分量作为 IMU 因子加入到因子图中。
雷达里程计因子
每接收一次新雷达数据,首先对整个点云进行特征提取,按照点的曲率提取其角点和平面点。对角点和平面点的筛选标准和方法可以参考:LOAM 论文阅读笔记 和 LeGO-LOAM 论文阅读笔记。记 $i$ 时刻提取出来的角点和平面点分别为:$F_i^e, F_i^p$。每一帧雷达观测由这两种特征点组成,记为:$\mathbb{F}_i = \{F_i^e, F_i^p\}$ (载体坐标系下)。和 LOAM 和 LeGO-LOAM 不同,LIO-SAM 使用了视觉 SLAM 中常用的关键帧的概念来减少计算量。LIO-SAM 中选择关键帧的标准很简单,只要计算出来该帧的位姿比上一个节点(上一个关键点对应的位姿)变化超过一定阈值时即作为新的关键帧加入因子图中。两个关键帧之间的所有雷达数据会被丢弃,算法中使用的位姿变化的阈值为 1m (位置)和 10° (姿态)。
下面来描述一下一个新的雷达里程计因子产生的过程,当一个新的载体状态节点 $\boldsymbol{x}_{i+1}$ 与其对应的该帧数据 $\mathbb{F}_{i+1}$ 被加入图中,过程如下:
- 利用滑动窗口中的关键帧建立局部体素地图
LIO-SAM 中维护一个滑动窗口来保持最近的 n 个关键帧(论文中 n = 25)进行优化。假设这个滑动窗口中的关键帧子集(sub-keyframes)为 $\{\mathbb{F}_{i-n}, ..., \mathbb{F}_{i} \}$。首先将这个子集中的关键帧利用每个节点在世界坐标系下的位姿 $\boldsymbol{T}$ 转换至世界坐标系下。然后将所有关键帧中的点云进行融合得到两个体素地图,分别是角点地图 $\boldsymbol{M}_i^e$ 和平面点地图 $\boldsymbol{M}_i^p$。即:
$$
\begin{aligned}
\boldsymbol{M}_i &= \{\boldsymbol{M}_i^e, \boldsymbol{M}_i^p\}\\
\boldsymbol{M}_i^e &= {}^{'}F^e_{i} \cup {}^{'}F^e_{i-1} \cup ... \cup {}^{'}F^e_{i-n}\\
\boldsymbol{M}_i^p &= {}^{'}F^p_{i} \cup {}^{'}F^p_{i-1} \cup ... \cup {}^{'}F^p_{i-n}
\end{aligned}
$$
上式中,${}^{'}F_{i}$ 表示被转换至世界坐标系下的特征点。为了减少重复特征点的计算,对融合后的点云进行降采样处理,对角点和平面点的采样分辨率分别是 0.2m 和 0.4m。
- 特征匹配
有了局部特征地图后,接下来使用新加入的关键帧特征点集 $\mathbb{F}_{i+1}$ 与局部地图中的特征点进行匹配。LIO-SAM 中使用的匹配方法和 LOAM 一致,这里不赘述细节,同样可以参考我对 LOAM 的阅读笔记。LIO-SAM 匹配时使用的相对运动预测值为 IMU 解算出来的运动估计。通过这个过程,对新的一帧中的每个特征点 ${}^{'}F^e_{i+1}, {}^{'}F^p_{i+1}$ 都找到了在 $\boldsymbol{M}_i^e, \boldsymbol{M}_i^p$ 的对应特征(角点特征由两个特征点组成,平面点由三个特征点组成)。
- 计算相对位姿变化
首先计算新的关键帧中每个特征点和其对应特征的距离,角点和特征点的距离计算方法分别如下所示:
$$
\begin{aligned}
\boldsymbol{d}_{e_k} &= \frac{|(\boldsymbol{p}_{i+1, k}^e - \boldsymbol{p}_{i, u}^e)\times(\boldsymbol{p}_{i+1, k}^e - \boldsymbol{p}_{i, v}^e)|}{|\boldsymbol{p}_{i, u}^e - \boldsymbol{p}_{i, v}^e|}\\
\boldsymbol{d}_{p_k} &= \frac{\begin{vmatrix}
(\boldsymbol{p}_{i+1, k}^e - \boldsymbol{p}_{i, u}^e)\\(\boldsymbol{p}_{i, u}^e - \boldsymbol{p}_{i, v}^e)\times(\boldsymbol{p}_{i, u}^e - \boldsymbol{p}_{i, w}^e)
\end{vmatrix}}{|(\boldsymbol{p}_{i, u}^e - \boldsymbol{p}_{i, v}^e)\times(\boldsymbol{p}_{i, u}^e - \boldsymbol{p}_{i, w}^e)|}
\end{aligned}
$$
上式的推导同样可以参考 LOAM 论文阅读笔记 中的特征匹配部分。接下来要做的就是通过高斯牛顿法求出一个新一帧在世界坐标系下的位姿使得所有特征的距离之和最小,即求解以下问题:
$$
\arg\min_{\boldsymbol{T}_{i+1}}\left\{\sum_{\boldsymbol{p}_{i+1, k}^e \in {}^{'}F_{i+1}^e}\boldsymbol{d}_{e_k} + \sum_{\boldsymbol{p}_{i+1, k}^p \in {}^{'}F_{i+1}^p}\boldsymbol{d}_{p_k}\right\}
$$
接下来计算出前后两帧相对位姿作为激光雷达里程计因子:
$$
\Delta \boldsymbol{T}_{i,i+1} = \boldsymbol{T}_i^T\boldsymbol{T}_{i+1}
$$
GPS 因子
为了消除长时间运行的累积漂移,当接收到 GPS 观测值时,首先将其转换至当地的笛卡尔坐标系,然后构建节点加入至因子图中,如果 GPS 和其他传感器没有经过硬件同步,则通过插值计算出该节点所处时间的观测值。实际使用中,由于漂移是缓慢积累的,所以不需要每个 GPS 都加入图中,因此 LIO-SAM 只在当前估计的位置协方差大于收到 GPS 位置的协方差时才将其加入图中。
回环因子
当一个新节点 $\boldsymbol{x}_{i+1}$ 加入因子图中,首先对图中之前的节点进行搜索,找出在笛卡尔坐标系下距离新节点比较近的节点。然后融合与该节点时间上相邻的若干个节点(论文中使用 12)的点云观测,构建一个局部体素地图。然后同样进行特征匹配。获得该帧与新加入关键帧的相对位姿变化,并作为回环因子加入图中。具体处理中,搜索距离设定为 15m。
实验
TODO
结论
TODO