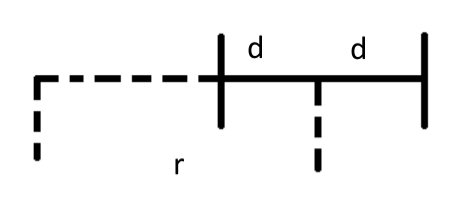>
返回
SLAM 激光SLAM Sensors

轮式里程计运动模型及标定

这篇博客主要整理了两轮差分底盘的运动模型以及怎么对里程计数据进行校正。

轮式里程计模型

两轮差分底盘的运动学模型

  1. 优点

    • 结构简单
    • 便宜，只需要两个电机（驱动器）
    • 模型简单，并且可以实现任何轨迹跟踪

  2. 差分模型及运动解算

    • 考虑两轮在做半径为r的圆周运动，v和w是底盘中心的线速度和角速度，$v_{L/R}$ 和 $\omega_{L/R}$ 分别对应左/右轮子的线速度和角速度，d为底盘中心离两侧轮子的距离，b为两轮之间的距离（b = 2d）
    • 目标：根据两轮的角速度（编码器测出的数据）以及其他参数求出底盘中心（机器人）运动的线速度v和角速度w
    • 求解：

据两轮绕圆周中心的角速度相等：

$$
\begin{aligned}
    \frac{v_L}{r - d} &= \frac{v_R}{r + d}\\
    \rightarrow v_L(r + d) &= v_R(r - d)\\
    \rightarrow (v_L - v_R)r &= (v_R + v_L)d\\
    \rightarrow r &= \frac{v_R + v_L}{v_R - v_L}d
\end{aligned}
$$

因此，

$$
\begin{aligned}
    r + d &= \frac{v_R + v_L}{v_R - v_L}d + d \\
    &= \frac{2v_R}{v_R - v_L}d
\end{aligned}
$$

根据底盘中心和两轮角速度相等：

$$\omega = \frac{v_R}{r + d} = \frac{v_R - v_L}{2d}$$

根据$v = \omega r$:

$$
\begin{aligned}
    \omega &= \frac{\omega_Rr_R - \omega_Lr_L}{2d}\\
    v = \omega r = \frac{v_R - v_L}{2d}\frac{v_R + v_L}{v_R - v_L}d &= \frac{v_R + v_L}{2} = \frac{\omega_Rr_R + \omega_Lr_L}{2}
\end{aligned}
$$

整理得

$$\begin{bmatrix}
    v \\ \omega
    \end{bmatrix} = 
    \begin{bmatrix} \frac{r_L}{2} & \frac{r_R}{2} \\
         -\frac{r_L}{b} & \frac{r_R}{b}\end{bmatrix}
         \begin{bmatrix}\omega_L \\ \omega_R
         \end{bmatrix} = J\begin{bmatrix}\omega_L \\ \omega_R\end{bmatrix}$$

轨迹推算（Dead Reckoning）

  1. 示意图

  2. 递推公式

假设

  • 当前位姿（世界坐标系下）为$(x, y, \theta)$
  • 运动增量（车体坐标系下）为$(dx, dy, d\theta)$

求解更新后的位姿

$$
\begin{bmatrix}x \\ y \\ \theta\end{bmatrix}
=\begin{bmatrix}x \\ y \\ \theta\end{bmatrix} + 
\begin{bmatrix}
\cos{\theta} & -\sin{\theta} & 0 \\
    \sin{\theta} & \cos{\theta} & 0 \\
    0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
dx \\
dy \\
d\theta
\end{bmatrix}
$$

加入噪声后

$$
\begin{bmatrix}x \\ y \\ \theta\end{bmatrix}=
\begin{bmatrix}x \\ y \\ \theta\end{bmatrix} +
 \begin{bmatrix}
 \cos{\theta} & -\sin{\theta} & 0 \\
  \sin{\theta} & \cos{\theta} & 0 \\
   0 & 0 & 1
 \end{bmatrix}
 \begin{bmatrix}
 dx + \epsilon_x \\
  dy + \epsilon_y \\
   d\theta + \epsilon_\theta
 \end{bmatrix}
 $$

噪声会随时间积累，所以dead reckoning精度会越来越低

轮式里程计标定

线性最小二乘的基本概念

  • 求解线性方程组 $Ax = b$，其中

    • $A$ 为 $m\times n$ 的矩阵
    • $x$ 为 $n\times 1$ 的向量
    • 当 $m > n$ 时为超定方程组，方程组无解。实际情况中进行slam时移动机器人约束条件远远多于状态维度，通常为此种情况，此时需要求解最小二乘解

  • 最小二乘解

    $x^*=(A^TA)^{-1}A^Tb$

线性最小二乘在里程计标定中的应用

  1. 主要方法包括：

    • 直接线性方法：通用性强，实现简单，精度不高（因此实际中比较少直接使用）
    • 基于模型的方法：精度高，实现复杂，特异性强（实际中较多使用）

  2. 直接线性方法

用激光雷达的scan-match数据作为真值$u_i^*$ 里程计测量数据为$u_i$ 假设两者成线性关系$u_i^* = Xu_i$，其中：

$$
X = \begin{bmatrix}
x_{11} & x_{12} & x_{13} \\
x_{21} & x_{22} & x_{23} \\
x_{31} & x_{32} & x_{33}
\end{bmatrix}
$$

标定过程就是求解$X$的过程（如何矫正里程计测量数据） 对于每一组数据，有以下关系：

$$
\begin{aligned}
u_{ix}x_{11} + u_{iy}x_{12} + u_{i\theta}x_{13} = u_{ix}^* \\
 u_{ix}x_{21} + u_{iy}x_{22} + u_{i\theta}x_{23} = u_{iy}^* \\
  u_{ix}x_{31} + u_{iy}x_{32} + u_{i\theta}x_{33} = u_{i\theta}^*
  \end{aligned}
$$

写成矩阵形式有：

$$
\begin{aligned}
    \begin{bmatrix}
    u_{i_x} & u_{iy} & u_{i\theta} & 0 & 0 & 0& 0 & 0 & 0\\
     0 & 0 & 0 &u_{i_x} & u_{iy} & u_{i\theta}& 0 & 0 & 0\\
     0 & 0 & 0& 0 & 0 & 0 &u_{i_x} & u_{iy} & u_{i\theta}
    \end{bmatrix}
    \begin{bmatrix}
    x_{11}\\
    x_{12}\\
    ... \\ 
    x_{33}
    \end{bmatrix} = 
    \begin{bmatrix}
    u^*_{ix} \\
    u^*_{iy} \\
    u^*_{i\theta}
    \end{bmatrix}\\
\rightarrow A_i\vec{X} = b_i
\end{aligned}
$$

对于所有n个数据点有：

$$
\begin{aligned}
    A = 
    \begin{bmatrix}A_1 \\ ...\\ A_n\end{bmatrix}\\
    b = 
\begin{bmatrix}
    b_1 \\ ... \\ b_n
\end{bmatrix}
\end{aligned}
$$

此时可以用最小二乘求解

  1. 基于模型方法

运动学模型

$$
\begin{bmatrix}
v \\ \omega
\end{bmatrix} = 
\begin{bmatrix} 
\frac{r_L}{2} & \frac{r_R}{2} \\
 -\frac{r_L}{b} & \frac{r_R}{b}
 \end{bmatrix}
\begin{bmatrix}\omega_L \\ \omega_R
\end{bmatrix} = J
\begin{bmatrix}
\omega_L \\ \omega_R
\end{bmatrix} = 
\begin{bmatrix}
J_{11} & J_{12} \\
 J_{21} & J_{22}
\end{bmatrix}
$$

知道 $v$ 和 $\omega$ 之后，可以根据采样时间积分求得机器人状态 $(x(t), y(t), \theta(t))$：

$$
\begin{aligned}
\theta(t) &= \int\omega(t)dt \\
x(t) &= \int v(t)\cos{(\theta(t))}dt \\
y(t) &= \int v(t)\sin{(\theta(t))}dt
\end{aligned}
$$

根据匀速运动假设（采样时间内机器人保持匀速运动），及运动学模型有：

$$
\begin{aligned}
\omega(t) = \omega &= J_{21}\omega_{L} + J_{22}\omega_{R} \\
v(t) = v &= J_{11}\omega_{L} + J_{12}\omega_{R} \\
J_{11} &= -\frac{b}{2}J_{21} \\
J_{12} &= \frac{b}{2}J_{22}\\
\rightarrow v(t) = v &= \frac{b}{2}(-J_{21}\omega_{L} + J_{22}\omega_{R})
\end{aligned}
$$

已知两轮的角速度 $\omega_L$ 和 $\omega_R$，需要求解两轮半径（$r_L$ 和 $r_R$）和两轮之间的距离 $b$

基本过程：

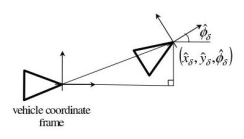
  • 假设激光雷达位于车体的正中心
  • 激光雷达的匹配值作为观测值
  • 里程计的积分值作为预测值
  • 通过最小化预测值和观测值的差即可得到里程计的参数
  • 里程计的积分值用$r_x$ , $r_y$ , $r_θ$ 表示，激光雷达的匹配值用 $s_x$ , $s_y$ , $s_θ$ 表示
  1. 具体求解过程

角度积分表达式(单一时间数据点)

$$
\begin{aligned} 
r_\theta(t) &=
    \int \omega(t)dt = \int J_{21}\omega_{L} + J_{22}\omega_Rdt \\
    r_\theta(t) &= (\omega_L\Delta T \:\:\: \omega_R\Delta T)
    (\begin{aligned}J_{21} \\J_{22}\end{aligned}) = s_\theta\\
    &\rightarrow A_0 J_2 = s_{\theta 0}
    \end{aligned}
$$

结合所有时间数据点可以求解 $Ax = b$，可以求得 $J_{21}$ 和 $J_{22}$ 在已知 $J_{21}$ 和 $J_{22}$ 的情况下，对里程计的位置积分可以表示成与参数b成线性关系（$\cos\theta_t$ 的积分可求）：

$$
\begin{aligned}
r_x(t) &= \int v(t) \cos{(\theta(t))} dt \\
&= \frac{b}{2}(-J_{21}\omega_{L} + J_{22}\omega_{R})\int \cos{(\theta(t))} dt \\
&= c_x b  = s_x\\
r_y(t) &= \int v(t) \sin{(\theta(t))} dt \\
&= \frac{b}{2}(-J_{21}\omega_{L} + J_{22}\omega_{R})\int \sin{(\theta(t))} dt \\
&= c_y b = s_y
\end{aligned}
$$

通过罗列所有时间点的约束方程，可以通过最小二乘求解两轮距离 $b$ 已知 $b, J_{21}, J_{22}$ 可以求得:

$$
\begin{aligned}
    r_L &= -J_{21}b\\
    r_R &= J_{22}b
\end{aligned}
$$

至此轮式里程计标定完毕

© 2020 - 2022 XT 的技术博客
Built with Hugo
Theme Stack designed by Jimmy