简介
这篇论文的中心思想是将一个复杂 SLAM 问题(同时定位和建图)分解成两个算法:一个算法以高频率运行,负责作为前端里程计来估计激光雷达(载体)的速度,但准确性相对较差;另一个算法则以相对低的频率运行作为后端进行激光雷达点云的匹配以及建图。此外,如果有 IMU 数据作为补充,可以将 IMU 的测量值作为里程计的初值来提高前端里程计的质量。这两个算法都会提取点云中边缘(sharp edge)和平面(plannar)的特征点,用来和建好的图中的边缘线特征以及平面特征进行匹配。对于里程计而言,这一步是通过快速计算得出的;而对于建图而言,这一步则是通过局部点云的几何分布并且和特征值和特征向量之间的关联来进行匹配的。
论文主要将原始的 SLAM 问题解耦成两部分:首先是在线运动估计,然后是通过批量优化(和 ICP 方法类似)进行建图来获取高精度的运动估计和地图。并且将这两个问题作为两个并行的算法来保证整体系统的实时性。
相关工作
相关工作比较久远,这里略过不提。
数学符号和任务描述
论文的任务是通过 3D 激光雷达的数据来进行载体运动估计和对经过路径的建图。
论文的假设前提:
- 激光雷达进行校正
- 激光雷达的线速度和角速度是平滑连续的
对于数学符号,右上标一般表示坐标系;雷达完整的一次扫描视为一次 sweep,文中用 $k, k\in\mathbb{Z}^+$ 来表示的序号,$\mathcal{P}_k$ 则为第 $k$ 次sweep对应的雷达点云数据。文中一共涉及两个坐标系:
- 雷达坐标系
$\{L\}$:原点在雷达的几何中心,$x$轴指向雷达左侧,$y$轴指向雷达上部,$z$轴指向雷达前方。激光雷达中的第$k$次sweep的点云中的第$i$个点在雷达坐标系的坐标记为$\boldsymbol{X}^L_{\{k,i\}}$ - 世界坐标系
$\{W\}$:全局坐标系,和最初的雷达坐标系重合。同理,激光雷达中的第$k$次sweep的点云中的第$i$个点在世界坐标系的坐标记为$\boldsymbol{X}^W_{\{k,i\}}$
待解决问题的数学描述:给定一个点云序列 $\mathcal{P}_k, k\in\mathbb{Z}+$,计算雷达在每一次sweep中的运动估计,并且通过 $\mathcal{P}_k$ 来对经过的环境进行建图。
系统总览
雷达硬件
论文中的验证实验使用的雷达是 Hokuyo UTM-30LX,视域为 180°,扫描分辨率为 0.25°,扫描速度为 40 线每秒。这里可以区分一下扫描 scan 和 sweep 的区别,一次扫描是从 -90° 到 90°,而一次 sweep 则是又若干次 scan 组成。硬件如下图所示。这种雷达和我们现在常用的激光雷达原理有很大差别,所以不用太过深入研究。只需要了解输出点云的基本结构即可,这会在下一部分介绍。
软件总览
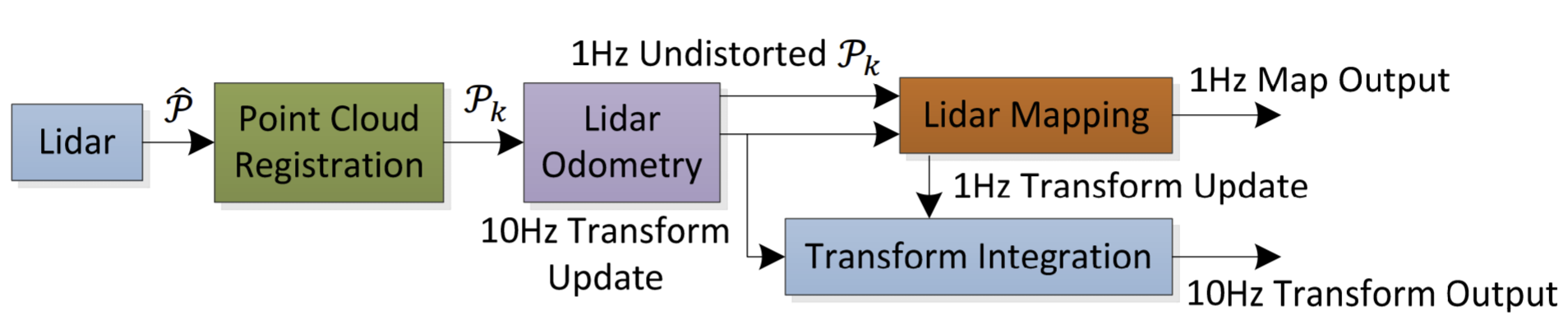
软件整体框图如下:
假设 $\hat{\mathcal{P}}$ 是在一次 scan 中获得的点,在每一次 scan 中 $\hat{\mathcal{P}}$ 在雷达坐标系中注册。完整的点云 $\mathcal{P}_k$ 由这一次 sweep 中所有的 $\hat{\mathcal{P}}$ 组合而成。然后两个算法对 $\mathcal{P}_k$ 进行处理。里程计算法以 10 Hz 的频率通过传进来的点云对前后两次的相邻的 sweep 的状态进行估计,通过这一步估计出的位姿变化被用来对激光雷达进行修正。此外,$\mathcal{P}_k$ 也被后端建图算法以 1 Hz 的频率进行处理,算法将修正后的点云对建好的地图进行匹配并扩充。最后通过两个算法产生的位姿变化以大约 10 Hz 的频率输出作为雷达位姿序列的一部分。
Lidar 里程计
特征点提取
激光雷达在单次扫描中的分辨率为 $0.25^\circ$,这些点会在一个扫描平面内。激光雷达旋转速度为 $180^\circ/s$ 并且以 $40$ Hz 的频率产生 scan(每一个 scan 对应一条线),因此可以算出扫描平面上垂直方向的分辨率为 $180^\circ / 40 = 4.5^\circ$。因此,只使用 $\mathcal{P}_k$ 中独立的扫描并且利用其共面的性质来提取特征点(不同扫描之间的点的关系不考虑)。
特征点提取的思路是希望提取点云中的属于边缘(如墙角)和平面的特征点。假定 $i$ 是 $\mathcal{P}_k$ 中的一个点,即 $i \in \mathcal{P}_k$,$\mathcal{S}$ 是这个点所属的扫描中与其相邻的连续点集。该点所处的局部平面的平滑程度由下式衡量:
$$
c = \frac{1}{|\mathcal{S}|||\boldsymbol{X}^L_{\{k, i\}}||}||\sum_{j\in\mathcal{S},j\neq i}(\boldsymbol{X}^L_{\{k, i\}} - \boldsymbol{X}^L_{\{k, j\}})||
$$
不难发现,点之间的差距越小(点的变化率越小),相应的 $c$ 值也越小,表明该位置越平滑。计算完一次扫描的所有点的 $c$ 之后根据这个值进行排序,边缘特征点从 $c$ 值较大的点中选取,平面特征点则从 $c$ 值较小的点中选取。为了尽量让选取特征点在环境中均匀分布,算法将一次扫描分成了四个子区域,每个子区域最多只能提供 2 个边缘特征点和 4 个平面特征点。对每一个区域的点,只有当其 $c$ 值越过(两种特征点的)阈值并且没有超过特征点上限时才能被作为特征点提取出来。
在选择特征点的同时,有一些点需要避免:
- 当一个点相邻的点都被选择的时候,为了特征点分布尽量均匀,这个点应该避免
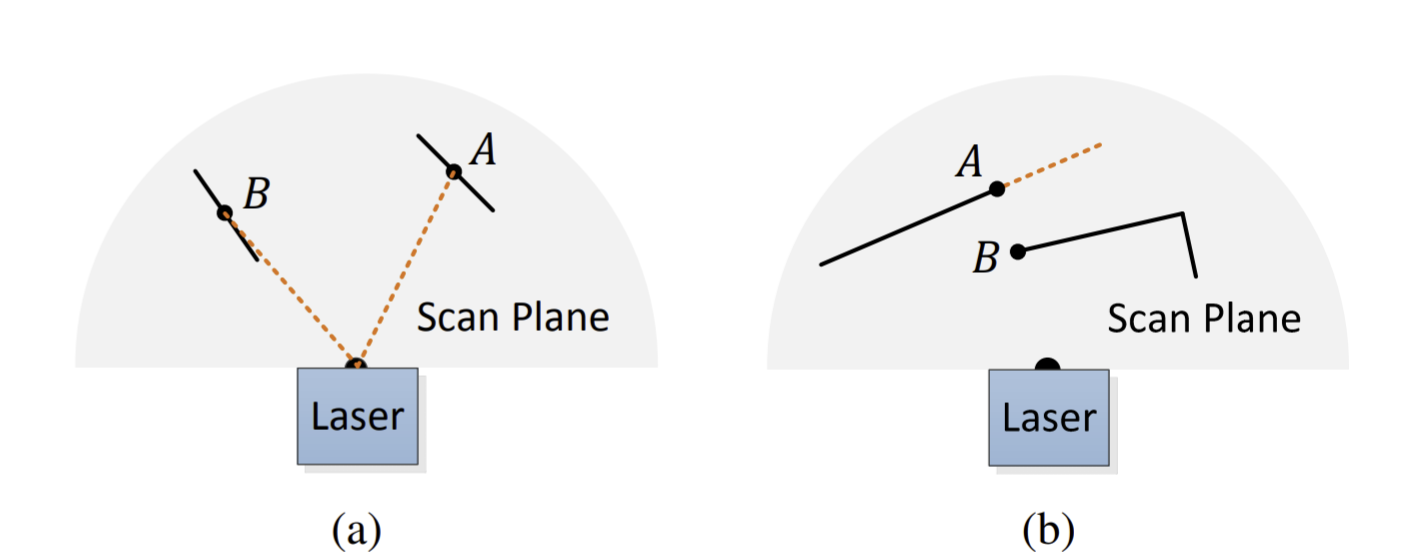
- 在和激光束几乎平行的平面上的点,这些点通常不太可靠,如下图(a) 中的点 B
- 遮挡区域边缘的点,同样的理由因为该点实际上处于被遮挡的区域,所以激光雷达位姿稍微变化之后就观测不到了,如下图 (b) 中的点 A。
为了保证上述的点不会被选择,同样可以利用点集 $\mathcal{S}$,首先对点集构建平面方程(对一次 scan 来说是直线方程)分析其是否和激光束平行;并且对每一个点集中的每个点分析,看其是否和点 $i$ 断连,并且断开连接的方向和激光束的方向一致,并且该点比 $i$ 离激光雷达近。(如上图(b) 中的点 B,点 A 作为 $i$,当找到点 $B$ 符合上面条件的时候,表示当前分析对象的点 $A$ 处于被遮挡区域边缘的点,应该避免)。
总体来说,只有当点 $i$ 通常上述的检查,并且其曲率值 $c$ 超过平面点或者角点的阈值,并且该区域的点没有达到上限时,它才会被选作特征点
一些边缘和平面特征点的例子如下所示,其中黄色点是边缘特征,红色点是平面特征。
特征点匹配
假设第 $k$ 次 sweep 的扫描时间为 $t_k$,当每一次 sweep 结束时,其对应的点云 $\mathcal{P}_k$ 会被重投影至 $t_{k+1}$,记为 $\bar{\mathcal{P}}_k$,然后我们会将它和在 $t_{k+1}$ 新接收到的点云 $\mathcal{P}_{k+1}$ 作比较来估计雷达的运动。
在这一部分里面首先假设 $\bar{\mathcal{P}}_k$ 和 $\mathcal{P}_{k+1}$ 已经有了,我们要做的是找到这两个点云的关联。对 $\mathcal{P}_{k+1}$ 进行特征点提取,分别记角点和平面点为 $\mathcal{E}_{k+1}$ 和 $\mathcal{H}_{k+1}$。对于 $\bar{\mathcal{P}}_k$,我们找到角点的线作为和 $\mathcal{E}_{k+1}$ 的关联以及平面作为 $\mathcal{H}_{k+1}$ 的关联。
值得注意的是,在完成一次 sweep 的过程中,由于激光雷达是一条线一条线扫的,并且扫的过程中,激光雷达也要运动。因此在每扫完一条线的时候,我们需要将对应的 $\mathcal{E}_{k+1}$ 和 $\mathcal{H}_{k+1}$ 利用目前估计的位姿变换重投影至扫描开始的时间,记为 $\bar{\mathcal{E}}_{k+1}$ 和 $\bar{\mathcal{H}}_{k+1}$,对其中的每一个点,我们要找到 $\bar{\mathcal{P}}_k$ 的最近点,为了提高搜索效率,这里$\bar{\mathcal{P}}_k$存储在 3D KD 树中。
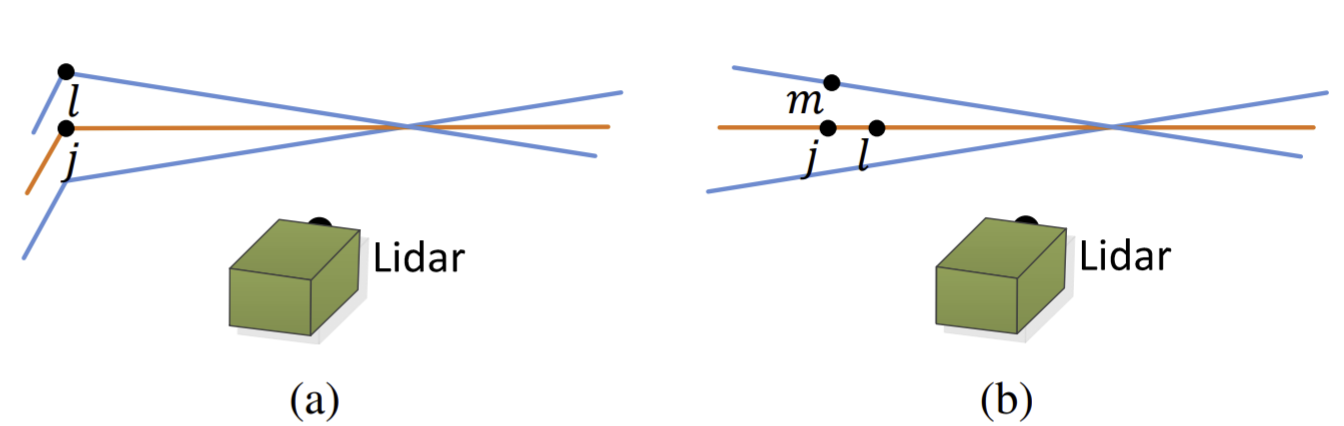
下图 (a) 中展示了对某一个角点而言,在前一个点云中找到其对应的边缘线的过程。假设 $i$ 为 $\bar{\mathcal{E}}_{k+1}$ 的一个角点,$j$ 为 $i$ 在 $\bar{\mathcal{P}}_k$ 最近的点,$l$ 则是 $j$ 所处的扫描线的相邻两条扫描线中,距离 $i$ 最近的点。这样 $(j,l)$ 就构成了角点 $i$ 在 $\bar{\mathcal{P}}_k$ 关联的边缘线了。此外我们要通过验证 $j, l$ 也是角点,验证方法同上一部分。另外,在上面的分析中,我们一般不会取两条不同的扫描线的点一起分析,这里我们这么做是因为对于一条扫描线而言,其位于一条边缘上的角点最多只有一个(一条横线和一条竖线的交点),因此我们只能取两条扫描线上的点构建边缘线。还有一种情况是当边缘线和扫描线重合的情况下扫描线上的所有点都是角点,但我们不考虑那种情况,因为通过那种方法检测到的边缘线并不稳定,当雷达位姿稍微变化之后它就变成平面上的一条线了。
上图 (b) 则展示了怎么找到一个平面点对应的平面。假设 $i$ 为 $\bar{\mathcal{H}}_{k+1}$ 的一个平面点,$j$ 为 $i$ 在 $\bar{\mathcal{P}}_k$ 最近的点,$l$ 则是在 $j$ 的扫描线上离 $i$ 第二近的点,$m$ 则是 $j$ 的两条相邻扫描线上离 $i$ 最近的点。这保证这三个点不共线,同样如果验证这三个点都是平面点后,则通过这三个点可以构造 $i$ 对应的平面特征。
在计算激光雷达的位姿的时候,我们需要最小化这些特征点和其关联的特征的距离。因此对角点和平面点找到其关联特征之后,需要计算特征点和关联点特征的距离。
对于角点,计算公式如下:
$$
d_{\mathcal{E}} = \frac{|(\tilde{\boldsymbol{X}}^L_{(k+1, i)} - \bar{\boldsymbol{X}}^L_{(k, j)})\times(\tilde{\boldsymbol{X}}^L_{(k+1, i)} - \bar{\boldsymbol{X}}^L_{(k, l)})|}{|\bar{\boldsymbol{X}}^L_{(k, j)} - \bar{\boldsymbol{X}}^L_{(k, l)}|}
$$
分子项为 $(i,j)$ 和 $(i, l)$ 的叉乘表示三角形 $ijl$ 的面积,然后将其除以 $(j,l)$ 的长度作为 $i$ 离 $(j,l)$ 的高即可以得到距离。
对于平面点,计算公式如下:
$$
d_{\mathcal{H}} = \frac{\left|\begin{aligned}
(\tilde{\boldsymbol{X}}^L_{(k+1, i)} &- \bar{\boldsymbol{X}}^L_{(k, j)})\\
(\bar{\boldsymbol{X}}^L_{(k, j)} - \bar{\boldsymbol{X}}^L_{(k, l)})&\times(\bar{\boldsymbol{X}}^L_{(k, j)} - \bar{\boldsymbol{X}}^L_{(k, m)})
\end{aligned}\right|}{|
(\bar{\boldsymbol{X}}^L_{(k, j)} - \bar{\boldsymbol{X}}^L_{(k, l)})\times(\bar{\boldsymbol{X}}^L_{(k, j)} - \bar{\boldsymbol{X}}^L_{(k, m)})|}
$$
上式 有两部分:$(j,l), (j, m)$ 叉乘 为该平面的一个法向量,然后计算任意一个点距该平面的距离,只需要将该点和平面上的一点连线再点乘法向量即可得到距离。
运动估计
根据前面一部分假设,激光雷达是以恒定线速度和角速度进行运动,因此我们对一次 sweep 中不同时间扫描的点的位姿可以进行线性插值。假设 $t$ 是当前时间点,$t_{k+1}$ 是第 $t+1$ 个扫描的时间戳。假设 $\boldsymbol{T}_{k+1}^L$ 是时间 $[t_{k+1},t]$ 之间的雷达位姿变换,其包含留个参数,分别是三个轴的平移分量和旋转分量,即 $\boldsymbol{T}_{k+1}^L = [t_x, t_y, t_z, \theta_x, \theta_y, \theta_z]$。对于 $\mathcal{P}_k$ 中的一个点 $i$,记 $t_i$ 为其对应时间,记 $\boldsymbol{T}_{(k+1,i)}^L$ 是时间 $[t_{k+1},t_i]$ 的位姿,我们通过线性插值得到,如下所示:
$$
\boldsymbol{T}_{(k+1,i)}^L = \frac{t_i -t_{k+1}}{t - t_{k+1}}\boldsymbol{T}_{k+1}^L
$$
为了将 $\mathcal{E}_{k+1}, \mathcal{H}_{k+1}$ 重投影得到 $\tilde{\mathcal{E}}_{k+1}, \tilde{\mathcal{H}}_{k+1}$,我们需要得到它们的空间几何关系,包括旋转和平移,如下所示:
$$
\boldsymbol{X}_{(k+1,i)}^L = \boldsymbol{R}\tilde{\boldsymbol{X}}_{(k+1,i)}^L + \boldsymbol{T}^L_{(k+1,i)}(1:3)
$$
上式中,$\boldsymbol{T}^L_{(k+1,i)}(1:3)$ 表示 $\boldsymbol{T}^L_{(k+1,i)}$ 的前三个分量,即平移分量,$\boldsymbol{R}$ 为旋转矩阵,由罗德里公式得到:
$$
\begin{aligned}
\boldsymbol{R} &= \exp{(\tilde{\omega}\theta)}\\
&= \boldsymbol{I} + \tilde{\omega}\sin{\theta} + \tilde{\omega}^2(1-\cos{\theta})
\end{aligned}
$$
上式中,$\theta$ 是旋转分量的模,$\omega$ 是旋转分量归一化后的单位向量,即:
$$
\begin{aligned}
\theta &= ||\boldsymbol{T}^L_{(k+1,i)}(4:6)||\\
\omega &= \boldsymbol{T}^L_{(k+1,i)}(4:6) / \theta
\end{aligned}
$$
而$\tilde{\omega}$ 为 $\omega$ 构造的反对称矩阵。结合上述信息,我们可以构建 $\mathcal{E}_{k+1}$ 中的角点和对应边缘线以及平面点和对应平面的几何关系,即:
$$
f_{\mathcal{E}}(\boldsymbol{T}^L_{(k+1,i)}, \boldsymbol{T}^L_{k+1}) = d_\mathcal{E},\quad i\in\mathcal{E}_{k+1}\\
f_{\mathcal{H}}(\boldsymbol{T}^L_{(k+1,i)}, \boldsymbol{T}^L_{k+1}) = d_\mathcal{H},\quad i\in\mathcal{H}_{k+1}
$$
最后,可以用 LM 方法来进行迭代求解获得雷达的运动关系:通过将 $\mathcal{E}_{k+1}, \mathcal{H}_{k+1}$ 中的每个点叠加在一起,可以获得如下非线性方程:
$$
\boldsymbol{f}(\boldsymbol{T}^L_{k+1}) = \boldsymbol{d}
$$
上式中,$\boldsymbol{f}$ 的每一行对应一个特征点,$d$ 中的对应行表示该特征点的距离。我们计算 $\boldsymbol{f}$ 相对于 $\boldsymbol{T}^L_{k+1}$ 的雅克比矩阵记为 $\boldsymbol{J}$, 即:$\boldsymbol{J} = \partial\boldsymbol{f}/\partial\boldsymbol{T}^L_{k+1}$,可以通过以下方法进行优化迭代使得 $\boldsymbol{d}$ 最小。
$$
\boldsymbol{T}^L_{k+1} \leftarrow \boldsymbol{T}^L_{k+1} - (\boldsymbol{J}^T\boldsymbol{J} + \lambda\mathrm{diag}(\boldsymbol{J}^T\boldsymbol{J}))^{-1}\boldsymbol{J}^T\boldsymbol{d}
$$
雷达里程计算法
雷达里程计整体算法如下图所示:
大致思路如下:
- 从上一次 sweep 获得输入点云
$\bar{\mathcal{P}}_k$,当前时间的点云(点的数量持续增加)$\mathcal{P}_{k+1}$,以及从上一时刻的位姿变化$\boldsymbol{T}^L_{k+1}$ - 从
$\mathcal{P}_{k+1}$提取角点和平面点$\mathcal{E}_{k+1}, \mathcal{H}_{k+1}$ - 对每一个特征点,在
$\bar{\mathcal{P}}_k$找到其对应的特征,并且计算其距离 - 对每一个特征点分配一个双平方权重,对于距离比较远的特征点将其权重降低,对于距离超过一定阈值的点直接放弃,将其权重设为 0
- 接下来求解位姿变化
- 进行迭代计算,直到收敛
- 当当前 sweep 完成时,
$\mathcal{P}_{k+1}$用当前估计的位姿投影到$t_{k+2}$中,如果 sweep 没有完成,则进入下一轮迭代。
Lidar 建图
建图算法频率较低,对每一次 sweep 只会执行一次,在 $k+1$ 次 sweep 完成时,里程计会产生一个校正后的点云的 $\bar{\mathcal{P}}_{k+1}$ 以及从 $[t_{k+1},t_{k+2}]$ 的位姿变化。建图算法将点云匹配以及投影到世界坐标系 $W$ 中。假设 $\mathcal{Q}_k$ 是第 $k$ 次 sweep 结束时累积的点云地图,$\boldsymbol{T}_k^W$ 是雷达在第 $k$ 次sweep 结束的时间即 $t_{k+1}$ 在世界坐标系下的位姿;通过里程计提供的位姿,建图算法可以利用 $t_{k+1}, t_{k+2}$ 之间的位姿变化,将 $T_k^W$ 更新至 $\boldsymbol{T}_{k+1}^W$,然后将 $\bar{\mathcal{P}}_{k+1}$ 投影至世界坐标系,记为 $\bar{\mathcal{Q}}_{k+1}$,然后算法优化 $\boldsymbol{T}_{k+1}^W$,对, $\bar{\mathcal{Q}}_{k+1}$ 和 $\mathcal{Q}_{k}$ 进行匹配。
匹配过程中,特征点的提取方法和里程计一样,但是为了保持准确性,提取的特征点数量是里程计的十倍。为了找到特征点和对应特征的关联,将点云 $\mathcal{Q}_K$ 以 $10\mathrm{cm}$ 尺寸的立方体存储。和 $\bar{\mathcal{Q}}_{k+1}$ 有相交的立方体被提取出来存储在一个 3D 的 KD 树里。我们在特征点周围的区域对 $\mathcal{Q}_k$ 的点进行搜索。设 $\mathcal{S}'$ 是特征点附近的点集,进行特征分析。
对角点来说,只保留 $\mathcal{S}'$ 中的边缘线中的点;对平面点,只保留 $\mathcal{S}'$ 中的平面的点。(每个点是边缘线的点还是平面的点在里程计已经判断过了)。然后计算 $\mathcal{S}'$ 的协方差矩阵,记为 $\boldsymbol{M}$,并计算该矩阵的特征值和特征向量,分别为 $\boldsymbol{V}$ 和 $\boldsymbol{E}$。假如 $\mathcal{S}'$ 分布在边缘线上,$\boldsymbol{V}$ 其中一个特征值会特别大,其对应的特征向量表示了这条边缘线的方向。另一方面,假如 $\mathcal{S}'$ 分布在平面上,$\boldsymbol{V}$ 其中一个特征值会特别小,其对应的特征向量表示了这条平面的方向。将$\mathcal{S}'$ 的几何中心代入该向量就可以得到该特征(边缘线或者平面)的具体位置(直线方程或者平面方程)。
下一步是计算特征点到对应特征的距离,这里我们在边缘线上选取两个点,平面上选取三个点。然后通过和里程计同样的方法计算其对应的距离,然后用同样的方式对位姿进行优化。为了使得点分布比较均匀,这里对点云地图用voxel滤波进行降采样, voxel 为 5cm 的立方体。
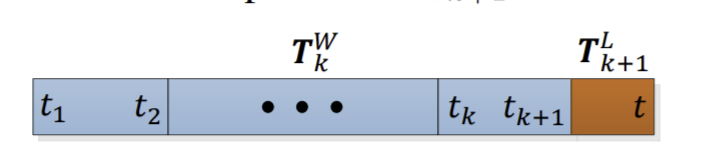
位姿变化关系如下图所示,蓝色区域表示每一次 sweep,产生一次对应的位姿 $\boldsymbol{T}_k^W$,橘色区域为 sweep 的过程中,里程计计算出的雷达在 sweep 过程中的变化$\boldsymbol{T}_{k+1}^L$,实时的雷达位姿可以通过 $\boldsymbol{T}_k^W$ 和 $\boldsymbol{T}_{k+1}^L$ 共同计算得到,其频率和里程计一致,为 10Hz。
实验
TODO
结论
TODO